Реферат: Анализ производственных функций

Линейная производственная функция

X=F(K,L)=E_K K+E_L L

Где E_K и E_L частные эффективности ресурсов.

E_K =-фондоотдача , E_L = - производитель труда.

Поскольку частные показатели эффективности имеют одинаковую размерность (точнее, одинаково безразмерны), то можно находить любые средние из них.

Эластичности замены труда фондами для линейной ПФ = ¥

эта величина показывает, на сколько процентов надо изменить фондо­вооруженность, чтобы добиться изменения нормы замены на 1%.

Производственная функция затраты-выпуск

X=F(K,L)=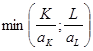

Где:

Коэффициенты эластичности представленные в виде логарифмических производных факторов показывают, на сколько процентов увеличится выпуск, если фактор возрастет на 1%. Например, согласно ПФ X=0,931K^0,539 L^0,594

при увеличении основных фон­дов (ОФ) на 1% валовой выпуск повысится на 0,539%, а при увеличе­нии занятых на 1% — на 0,594%.

Практическая часть

Задача

Дана производственная функция валового внутреннего продукта США по данным 1960-1995 гг.

X=2,248K^0,404 L^0,803

Валовой внутренний продукт США, измеренный в млрд. дол. в ценах 1987 г. возрос с 1960 по 1995 г. в 2,82 раза, основные производственные фонды за этот же период увеличились в 2,88 раза, число занятых - в 1,93 раза.

Необходимо рассчитать масштаб и эффективность производства.

Решение

Из условия x = 2,82 k =2,88 l =1,93;

('начала находим относительные эластичности по фондам и труду

Затем определяем частные эффективности ресурсов

после чего находим обобщенный показатель эффективности как среднее геометрическое частных: