Информатика / Реферат: Автоматическое управление. Следящие системы

Реферат: Автоматическое управление. Следящие системы

Для определения устойчивости САР используют критерии устойчивости, т.е. с помощью них можно определить устойчива ли система или нет, не прибегнув к решению больших задач с использованием дифференциальных уравнений.

Для решения проблем корректирования следящей системы с помощью дифференцирующей фазоопережающей цепи можно пользоваться тремя методами:

- аналитический метод (критерий устойчивости Рауса-Гурвица).

На практике критерий Гурвица обычно применяют для проверки устойчивости систем невысокого порядка, так как при высоком порядке расчеты условия устойчивости становятся очень громоздкими. Данный метод позволяет судить об устойчивости замкнутой системы по положительным коэффициентам характеристического уравнения без громоздких решений. Необходимые и достаточные уравнения устойчивости системы определяются соотношениями коэффициентов, зависящих от порядка системы;

- графо-аналитический метод (критерий устойчивости Михайлова).

Данный метод основан на связи характера переходных процессов систем с амплитудой и фазой вынужденных колебаний, устанавливающихся при синусоидальном воздействии. Анализ устойчивости сводится к построению комплексной частотной характеристики по характеристическому многочлену замкнутой системы. Формулировка данного метода: “Для устойчивости линейной системы необходимо и достаточно чтобы годограф при изменении частоты ω от 0 до ∞ начинался на вещественной оси в точке a 1 и проходил последовательно против часовой стрелки n -квадрантов комплексной плоскости, не обращаясь в 0 и стремясь к ∞ в n -квадранте, где n – порядок системы.” Критерий устойчивости Михайлова имеет недостаток, который заключается в том, что при увеличении порядка системы (например, начиная с 4-го) резко возрастает объем вычислений;

- графо-аналитический метод (критерий устойчивости Найквиста).

Критерий Найквиста позволяет судить об устойчивости по амплитудно-фазовым характеристикам разомкнутой системы. Этот метод применим для систем, устойчивых в разомкнутом состоянии. Формулировка: “Для устойчивости системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении частоты ω от 0 до ∞ не охватывала точку с координатами {-1 ; j 0 }.” Если нет местных обратных связей, то замкнутая система будет устойчивой при условии, что она состоит из устойчивых звеньев.

- критерий устойчивости Найквиста с использованием ЛЧХ.

Применение аналитического и графического критериев Найквиста на логарифмической плоскости приводят к более наглядной оценке устойчивости и запасов устойчивости по фазе и модулю. Формулировка: “Для устойчивости замкнутой системы необходимо и достаточно чтобы на всех частотах, где ЛАЧХ разомкнутой системы положительная (L(ω)>0), фазовый сдвиг не достигал значения -π(180°) или достигал его четное число раз. Замкнутая система будет находиться на границе устойчивости, если на частоте ω c , ЛАЧХ разомкнутой системы обращается в 0 .”

Для того чтобы скорректировать следящую систему целесообразно использовать графо-аналитический метод с использованием логарифмических частотных характеристик (ЛЧХ), так как при этом методе оптимизации следящей системы более хорошо видны погрешности характеристик ЛЧХ графиков и другие недостатки работы системы. При всем этом, проанализировав графики и изменяя отдельные характеристики системы, можно добиться совпадения текущих параметров с требуемыми.

2 Расчётная часть

2.1 Разработка структурной схемы

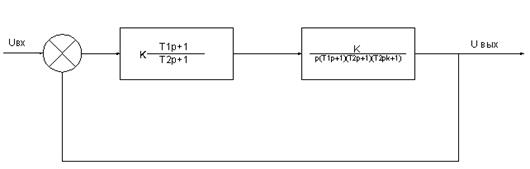
Для следящей системы необходимо высокое быстродействие и реагирование на изменяющиеся процессы в системе, увеличить коэффициент усиления системы k при сохранении достаточного запаса устойчивости по фазе, как об этом говорилось в разделе 1.3. И только при последовательном включении дифференцирующего фазоопережающего устройства с коэффициента усиления системы k при сохранении достаточного запаса устойчивости по фазе. Действительно, передаточная функция скорректированной системы при этом будет иметь вид: