Реферат: Автоматизированный корреляционно-регрессионный анализ взаимосвязи статистических данных в среде
Выполнил: ст. III курса гр. 3
Широких Е.Б.
Проверил: доц. Левчегов О.Н.
Липецк 2011 г.
1. Постановка задачи статистического исследования
Корреляционно-регрессионный анализ взаимосвязи признаков является составной частью проводимого статистического исследования деятельности 30-ти предприятий и частично использует результаты ЛР-1.
В ЛР-2 изучается взаимосвязь между факторным признаком Среднегодовая стоимость основных производственных фондов (признак Х ) и результативным признаком Выпуск продукции (признак Y ), значениями которых являются исходные данные ЛР-1 после исключения из них аномальных наблюдений.
| Исходные данные | ||
| Номер предприятия | Среднегодовая стоимость основных производственных фондов, млн.руб. | Выпуск продукции, млн. руб. |
| 5 | 1205,00 | 945,00 |
| 23 | 1299,50 | 1255,50 |
| 27 | 1407,50 | 1080,00 |
| 1 | 1448,00 | 1390,50 |
| 8 | 1502,00 | 1485,00 |
| 32 | 1529,00 | 1566,00 |
| 22 | 1637,00 | 1336,50 |
| 19 | 1677,50 | 1282,50 |
| 2 | 1704,50 | 1525,50 |
| 3 | 1758,50 | 1701,00 |
| 13 | 1772,00 | 1809,00 |
| 26 | 1812,50 | 1660,50 |
| 9 | 1839,50 | 1741,50 |
| 4 | 1853,00 | 1890,00 |
| 28 | 1893,50 | 1687,50 |
| 17 | 1907,00 | 1728,00 |
| 6 | 1947,50 | 1620,00 |
| 14 | 1947,50 | 1971,00 |
| 25 | 1947,50 | 1755,00 |
| 7 | 2001,50 | 2187,00 |
| 31 | 2082,50 | 1755,00 |
| 18 | 2109,50 | 2052,00 |
| 10 | 2123,00 | 2173,50 |
| 20 | 2136,50 | 1755,00 |
| 24 | 2177,00 | 2011,50 |
| 29 | 2190,50 | 1849,50 |
| 15 | 2231,00 | 2389,50 |
| 12 | 2325,50 | 2295,00 |
| 21 | 2379,50 | 2362,50 |
| 16 | 2555,00 | 2565,00 |
В процессе статистического исследования необходимо решить ряд задач.
1. Установить наличие статистической связи между факторным признаком Х и результативным признаком Y графическим методом.
2. Установить наличие корреляционной связи между признаками Х и Y методом аналитической группировки.
3. Оценить тесноту связи признаков Х и Y на основе эмпирического корреляционного отношения η .
4. Построить однофакторную линейную регрессионную модель связи признаков Х и Y , используя инструмент Регрессия надстройки Пакет анализа, и оценить тесноту связи признаков Х и Y на основе линейного коэффициента корреляции r .
5. Определить адекватность и практическую пригодность построенной линейной регрессионной модели, оценив:
а) значимость и доверительные интервалы коэффициентов а0 , а1 ;
б) индекс детерминации R2 и его значимость;
в) точность регрессионной модели.
6. Дать экономическую интерпретацию:
а) коэффициента регрессии а1 ;
б) коэффициента эластичности К Э ;
в) остаточных величин ε i .
7. Найти наиболее адекватное нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм .
2. Выводы по результатам выполнения лабораторной работы
Задача 1 . Установление наличия статистической связи между факторным признаком Х и результативным признаком Y графическим методом.
Статистическая связь является разновидностью стохастической (случайной) связи, при которой с изменением факторного признака X закономерным образом изменяется какой–либо из обобщающих статистических показателей распределения результативного признака Y.
Вывод:
Точечный график связи признаков (диаграмма рассеяния, полученная в ЛР-1 после удаления аномальных наблюдений) позволяет сделать вывод, что имеет место статистическая связь. Предположительный вид связи – линейная прямая.
Задача 2. Установление наличия корреляционной связи между признаками Х и Y методом аналитической группировки.
Корреляционная связь – важнейший частный случай стохастической статистической связи, когда под воздействием вариации факторного признака Х закономерно изменяются от группы к группе средние групповые значения 
результативного признака Y (усредняются результативные значения 
, полученные под воздействием фактора 
). Для выявления наличия корреляционной связи используется метод аналитической группировки.
Вывод:
Результаты выполнения аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных производственных фондов даны в табл. 2.2 Рабочего файла, которая показывает, что с увеличением значений факторного признака Х закономерно увеличиваются средние групповые значения результативного признака . Следовательно, между признаками Х и Y существует корреляционная связь.
Задача 3. Оценка тесноты связи признаков Х и Y на основе эмпирического корреляционного отношения.
Для анализа тесноты связи между факторным и результативным признаками рассчитывается показатель η – эмпирическое корреляционное отношение, задаваемое формулой
,
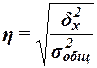--> ЧИТАТЬ ПОЛНОСТЬЮ <--