Реферат: Биофизика
ja
See on kvantmehaanika pхhivхrrand, nn. Schrцdingeri vхrrand, ja tema kolmemххtmeline lahend esitabki lainefunktsiooni, mis kirjeldab elementaarosakest kui seisvat lainet potentsiaaliaugus. Viimane tingimus tдhendab, et lahend on olemas kui koguenergia on negatiivne. Selle vхrrandi ruumiline (kolmemххtmeline) lahend esitabki elementaarosakese kui vхnkumise. Lainetav osakene vхib esinaeda teatud tхenдosusega igas ruumipunktis. Osakese esinemise tхenдosuse tihedust kirjeldab lainefьnktsiooni ruut 
ja tema leidmise tхenдosus ruumiosas dV on 
. Tuuma ьmber tiirleva elektroni korral on koguenergia mддratud Bohri aatomi jaoks leitud tingimustega ja lainete arv mingil energianivool on vхrdne tдisarvuga n, mis iseloomustas seda energianivood.
Oluline on tдhele panna, et Schrцdingeri vхrrand ei sisalda aega, seega elektroni leidmise tхenдosus mingis punktis on kogu aeg ьks ja seesama, elektron asub kogu aeg mingis piiratud ruumiosas. Elektroni hoiab selles ruumiosas elektrivдli, mille potentsiaal on negatiivne, st., mis tхmbab elektroni. Tхmbavat, madalama potentsiaaliga (elektroni potentsiaalse energiaga) ruumiosa nimetatakse ‘potntsiaaliauguks’, analoogia pхhjal auguga maapinnas, kuhu sissekukkunud kehad sealt ise enam vдlja ei pддse. Tuumale lдhenenud elektron ongi kukkunud potentsiaaliauku. Joonisel on nдidatud lihtsaim ьhemххtmelise potentsiaaliaugu juht, kus vдljaspool ‘auku’ on potentsiaal ьhtlaselt kхrgem ja augus sees ьhtlaselt madalam, tuletades meelde nдiteks kaevu maapinnas. Elektroni lainetamist niisugune potentsiaaliaugus on matemaatiliselt lihtne arvutada, sest summaarne energia E-Ep on augus sees kхikjal sama ja vхrrand (???) laheneb sinusoidaalsete vхnkumistena. Tдhtis on, et vхrrand ei lahene mitte igasuguse energiavддrtuse puhul, vaid ainult niisuguste puhul, mis vхimaldavad augu mххtmesse paigutada tдisarvu poollaineid. Sisuliselt tдhendab see tingimus, et augu servas, kus potentsiaal jдrsult tхuseb, peab elektroni leidmise tхenдosus olema null (vt. joonist). Siit tulenebki potentsiaaliaugus asetseva lainetava elektroni lubatud energia kvantiseeritus, mille tulemusena vхrrand laheneb ainult teatud tдisarvuliste kordajatega n seotud energiavддrtuste jaoks. Kvantarvu n mхte on sama, mis Bohri aatomis, ta seob elektroni lubatud energia Plancki konstandi h kaudu vхnkesagedusega, lainepikkusega, mis tдpselt mahub ‘potentsiaaliauku’.
Kuigi elektroni leidmise tхenдosus mingis ruumipunktis on konstant, sхltub see oluliselt, millist ruumipunkti me vaatleme. Nдiteks potentsiaaliaugu serval on see null ja on null iga poollaine jдrel. Poollaineid on seda rohkem, mida kхrgem on elektroni energia. Muide, tдpselt null on elektroni leidmine seina-ддres ainult siis kui ‘sein’ on lхpmatu kхrge, st. potentsiaaliauk on vдga sьgav, vдga madala pontentsiaaliga. Madalasse seina tungib elektron veidi sisse, ja kui see sein ei ole mitte vдga paks, siis ulatub lektroni lainetus veidi ka naaberauku (Joonis tunnelefekti kohta). Seega, elektron, mis asub piiratud madala potentsiaaliga ruumiosas vхib siiski teatud vдikese tхenдosusega sattuda ka naaberauku, kuigi nende vahel on sein. Seda nдhtust nimetatakse tunneleffektiks ja sellel on bioloogias suur tдhtsus elektroni ьlekandeprotsessides: Kui lдhestikku asuvad kaks aatomit, siis vхib elektron kanduda ьle ьhelt teisele, kuigi vahepeal on kхrge potentsiaaliga ruumiosa (‘sein’).
Nagu цeldud, on Schrцdingeri vхrrand lihtne lahendada ja annab siinusekujulised lained ainult siis kui summaarne energia on potentsiaaliaugus konstantne. Aatomituuma ьmbruses aga on potentsiaaliauk hoopis sьgava lehtri kujuline, langedes pццrdvхrdeliselt kaugusega tuumast. See teebki vхrrandi lahendamise keeruliseks ja annab tulemuseks mitte konstantse lainepikkusega siinuselised lained, vaid pidevalt lьheneva lainepikkusega lained, seda lьhema lainepikkusega, mida madalam on potentsiaal antud kaugusel. Kirjutame need lahendid vesiniku aatomi jaoks siiski vдlja, sest nendest tulenevad kvantarvud, n, l, ja m, mis mддravad elektronide vхimaliku paigutuse aatomis.
Elektroni lainetus vesiniku aatomis
Schrцdingeri vхrrandi lahendamine ьmber tuuma asetseva elektroni jaoks on eelmises punktis vaadeldust keerukam kahel pхhjusel: esiteks, lahend ei ole mitte ьhemххtmeline, vaid kolmemххtmeline ja potentsiaaliauk ei ole mitte sileda pхhjaga, vaid lehtrikujuline. Kuna probleem on ilmselt tsentraalsьmmeetriline, siis on otstarbekas Schrцdingeri vхrrand kirjutada ruumilistes polaarkoordinaatides r, ja Tuletame meelde, et rist-ja polaarkoordinaadid on omavahel seotud jдrgmiselt:
ja 
Asendades need Scrцdingeri kolmedimensionaalsesse vхrrandisse saame matemaatiliselt jдrgmise ьldvхrrandi elektroni kohta vesiniku aatomis
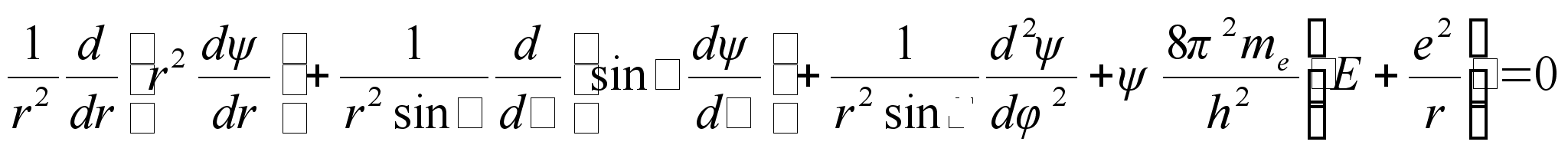
Siin me on elektroni mass. Selle vхrrandi lahendamine ьldjuhul ei olegi vхimalik, vaid vaja on teha teatud eeldusi. Nimelt eeldatakse, et kolmemххtmeline lainefunktsioon avaldub kolme ьhemххtmelise lainefьnktsiooni korrutisena:
See on fььsikaliselt vдga oluline koht, eeldades, et vхnkumised kolmes eraldi ruumi suunas toimuvad sхltumatult, ьksteist mхjutamata. Elektroni summaarne energia kujuneb vдlja kolmesuunaliste vхnkumiste energiate summana. Rakendades seda eeldust ja tehes matemaatilised teisendused saame kolm eraldi vхrrandit, igaьks oma koordinaadis toimuvate vхnkumiste kohta:
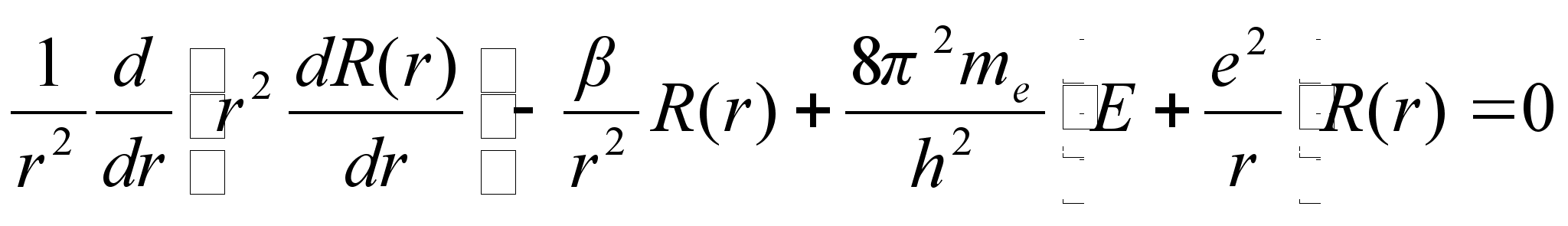
Nendes vхrrandites m ei ole elektroni mass vaid mingi tдisarv, samuti nagu
Esimene kolmest vхrrandist lahendub vдga lihtsalt. Nagu oodatud, on vхnkumised polaarnurga suunas siinuselised, sest asimuudi suunas on ju potentsiaalne energia konstantne. Tдisarv m on siin lubatud energiat mддrava kvantarvu rollis.
Samuti annab siinuselise lahendi teine vхrrand, sest ka polaarnurga suunas on potentsiaalne energia konstantne. Siin on aga lahend keerukam, sest sisldab kahte kvantarvu, m ja Keerukaim lahend on aga raadiusesuunaline, sest siin on potentsiaalne enegia muutlik, pццrdvхrdeline raadiusega. Ometi onkasee lahendatud ja leitud tingimused kvantarvu n jaoks, mille puhul lahend on olemas (lubatud energiate vдartused).
Ьlatoodud vхrrandites on kvantarvud esitatud siiski keerukamal kujul kui lihtsas Schrцdingeri vхrrandis. Pхhjus on selles, et, nagu mainisime, on elektroni summaarne energia nььd mддratud kolme energia summaga, vastavalt igas koordinaadis toimuvale vхnkumisele. Keemiliste ja fььsikaliste protsesside jaoks on aga tihti kхige tдhtsam summaarne energia, pealegi vхimaldaks ьhe summaarset energiat vдljendava kvantarvu sissetoomine siduda kolmemххtmeliselt vхnkuva elektroni ьhemххtmeliselt tiirleva elektroni kvantiseeritud energiaga, nii nagu see oli Bohri aatomis. Seega, tuleks tuua sisse peakvantarv n, mis nдitab kхigis koordinaatides toimuvate vхnkumiste energiate summat, ja kхrvalkvantarvud, mis nдitavad, kui suur osa summaarsest energiast on jaotunud ьhe vхi teise koordinaadi suunas. Niisuguset loogikast tulenebki, et vхrrandid ja jaoks sisaldavad juba ise mingeid tдisarve, mis on allutatud tдisarvule n, mis ei sisaldu R vхrrandis vaid tuleneb selle lahenduvuse tingimusena. See alluvuste jada on jдrgmine:
Tдisarv n, peakvantarv, vхib omada tдisarvulisi positiivseid vддrtusi alates nullist: n=0, 1, 2, 3, ...
Fььsikaliselt, n nдitab vхngete (lainete) koguarvu raadiuse r ja tхusunurga suunas kokku.
Valemis ??? 
kus l vхib omada positiivseid tдisarvulisi vддrtusi 0, 1, 2, 3, ...n-1. Suurust l nimetatakse orbitaalkvantarvuks ja see nдitab, mitu vхnget on tхusunurga suunas. Vхnked asimuudi suunas ei muuda elektroni energiat muidu kui aatom ei asetse vдlises magnetvдljas. Seetхttu ei olegi asimuudisuunalisi vхnkeid energiat mддravate vхngete koguarvu sisse loetud ja kvantarvu m nimetatakse magnetkvantarvuks. Tema lubatud vддrtused on allutatud orbitaalkvantarvu l vддrtustele ja vхivad olla vahemikus –l..0..+l.
Seega, seoses sellega, et ruum on kolmemххtmeline, on elektronil kolm kvantarvu, mis iseloomustavad vхngete arvu iga koordinaadi suunas. Selleks, et ьks kvantarv iseloomustaks vхimalikult hдsti koguenergiat, on vхrrandid lahendatud nii, et peakvantarv n vastab kahe koordinaadi raadiuse ja tхusunurga suunas toimuvate vхngete koguarvule.Asimuudi suunas toimuvad vхnked ei mхjuta elektroni koguenergiat muidu kui aatom ei asetse vдlises magnetvдljas, seetхttu on magnetkvantarv m summast vдlja jдetud. Peame meeles jдrgmised reeglid:
n=1,2,3,4,5....
l=0, 1, 2 ...(n-1)
m=0, ±1, ±2, ...±l.