Реферат: Биологическое время и его моделирование в квазихимическом пространстве

С помощью различных приближений [11] система уравнений четвертого порядка может быть редуцирована до второго. Такая система достаточно информативна и позволяет качественно, а во многих случаях и количественно, описать развитие популяций различных видов.

Рассмотрим редуцированную модель (1) из двух стадий – роста и деления, дополненных стадией самоингибирования:

C1 +M1 ® Cm	(p)
Cm +M2 ® fC1	(b)
C1 ® Cd	(g)
C1 +Cm ® Ca +C1	(a)	(11)
C1 « EE	(w1 )
C1 +X1 « (C1 X11 )	(d11 )
C1 +X2 « (C1 X12 )	(d12 )
Cm +X1 « (Cm X21 )	(d21 )
Cm +X2 « (Cm X22 )	(d22 )

Здесь использованы те же обозначения, что и в системах (6) – (9) (индексы опущены): С₁ – множество клеток разного возраста до митоза, С_m – митотические клетки; C_a – клетки в анабиозе; (C_k X_l ) – ингибированные клетки разных стадий; M₁ , M₂ –субстраты.

Следует отметить, что двухстадийный цикл (фазы S и M) наблюдается на ранних стадиях развития зародышей пойкилотермных животных [15, 16]. На этом основании в этот период в качестве единичного интервала времени можно использовать длительность t_c клеточного цикла («детлаф»).

В предположении постоянства концентраций субстратов М₁ , М₂ кинетика цепного роста популяции, состоящей из особей С₁ и С_m , описывается системой:

dc1 /dt = – px c1 + f b cm + w1	( 12.1 )
dcm /dt = p c1 – bx cm – a c1 cm	( 12.2 )

Здесь c₁ , c_m – количества растущих и митотические клеток; a, b, p –коэффициенты автоингибирования, рождения и роста популяции в отсутствии ингибиторов. В коэффициенты р и b включены постоянные количества субстратов М₁ и М₂ . f - коэффициент размножения. Коэффициенты b_x и p_x – функции количества ингибиторов x₁ и x₂ :

px = p+d1 ; bx = b + d2 , где d1 = d11 x1 + d12 x2 ; d2 = d21 x1 + d22 x2 . (13)

Система уравнений (12) представляет собой закон обобщенного движения двухстадийной популяции в пространстве состояний. Преобразованная в виде:

dc1 = (-px c1 + f b cm + w1 ) dt, dcm =(p c1 - bx cm - a c1 cm ) dt, ( 12а )

система (12) определяет соотношение между интервалами биологического dc_i и физического dt времени.

В приближении квазистационарности для митотических клеток С_m система (12.1-12.2) сводится к одному уравнению:

dc1 /dt=px c1 (K1 –c1 )/(K2 + c1 ) + w1	(14)
Здесь K1 =c1 ``=(f b p - px bx )/(a px ); K2 =bx /a.	(15)

Динамику численности популяции с₁ (t) в общем случае нельзя выразить в виде явной функции от времени t. Поэтому используют обратную функцию t(c₁ ), получаемую интегрированием (14) по с₁ :

t(c1 )=ln{(c1 /c0 )[(K1 -c0 )/(K1 -c1 )](1+n) }/(npx ), где n= K1 /K2 . (16)

Уравнение (16) в явном виде отображает физическое время на множество состояний популяции.

6. Интерпретация модели (I-компонент теории, interpretation).

На рис.1 приведены экспериментальные точки и графики функции (16), описывающие дрожжевых клеток в присутствии солей хрома и никеля [13]. При расчете графиков брали значения a, b, р , f, определенные по экспериментальным данным [17]. В пределах точности измерений расчетные кривые согласуются с экспериментом при измененении численности примерно на шесть порядков.

Хорошее согласие теории с экспериментом получено и для других биологических объектов [8, 9]. Поэтому интересно провести верификацию квазихимической модели по характеристикам, связанным с проблемами биологического времени.

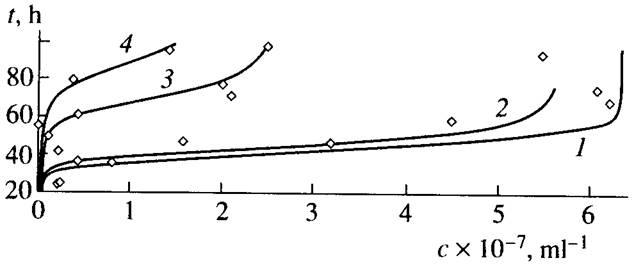
Рис.1. Экспериментальные точки и графики функции (16), описывающие рост пивных дрожжей при разных концентрациях (ммоль/л) солей хрома и никеля [13]: (1) c(Ni) = c(Cr) = 0.0, (2) c(Ni) = 0.5, (3) c(Cr) = 0.5, and (4) c(Ni) + c(Cr) = 0.5 + 0.5. Коэффициенты: a=1.25.10^-7 мл /ч, b=0.8ч^-1 , р=0.32 ч^-1 , f =2.

Уравнения (12a) можно представить в виде:

dc1 = Kc1 dt, dcm = Kcm dt,

( 17)

где величины K_c1 =(-p_x c₁ +f b c_m +w₁ )и K_cm = (p c₁ -b_x c_m -a c₁ c_m )представляют собой калибровочные коэффициенты для перехода от интервала физического времени dt к интервалам биологического времени dc_j .

На основе (17) получают соотношение между конечными временными интервалами:

D c1 =c1 dt, D cm =ИНТЕГРАЛ( Kcm dt ).

( 17а)

Калибровочные соотношения (17) обладают следующими свойствами:

1. Коэффициенты K_c1 и K_cm зависят от кинетических констант, характеризующих внутри- и внесистемные взаимодействия. Это определяет специфику биологического времени данного объекта.

2. Коэффициенты K_c1 и K_cm зависят от наблюдаемого состояния объекта, то есть изменяются при движении по фазовой траектории.

3. Коэффициенты K_c1 и K_cm неодинаковы для однотипных элементов данного уровня иерархии. Это означает, что собственное время «течет» с разной скоростью не только на разных уровнях биологической системы, но и в различных элементах одного уровня.

Приращение суммарной массы dm_p или численности dN_p популяции определяют интервал биологического времени популяции в целом. Для двухстадийной популяции dN_p = V(с₁ +с_m ), где V – объем системы. Связь между популяционным и физическим временем согласно (17) определяется соотношением:

dNp = V( Kc1 + Kcm )dt .

( 18)

Через длительность клеточного цикла t_c в физической шкале (в «детлафах») эта величина выразится в виде:

dNpd = V( Kc1 + Kcm )dt / tc .

(19)

Длительность клеточного цикла t_c в физической шкале рассчитывают либо по экпериментальным значениям прироста массы или численности клеток, либо по экпериментальным значениям параметров b и p модели (12).

Приращение численности популяции D с₁₂ =c₂ -c₁ в единице обьема наблюдается за время D t₁₂ =t₂ -t₁ , согласно (16) равное:

D t12 =ln{(c2 /c1 )[(K1 -c1 )/(K1 -c2 )](1+n) }/(npx ),

(20)

где c₁ ,c₂ – численности в моменты t₁ ,t₂ .

Среднее число делений n₁₂ каждой из c₁ клеток за это время равно:

n12 = log(c2 /c1 )/log2

(21)

Следователъно, t _c можно оценить по формуле:

tc = D t12 / n12

(22)