Реферат: Частотные и переходные характеристики систем авторегулирования
Введение
Радиопередающие устройства (РПдУ) применяются в сферах телекоммуникации, телевизионного и радиовещания, радиолокации, радионавигации. Стремительное развитие микроэлектроники, аналоговой и цифровой микросхемотехники, микропроцессорной и компьютерной техники оказывает существенное влияние на развитие радиопередающей техники как с точки зрения резкого увеличения функциональных возможностей, так и с точки зрения улучшения ее эксплуатационных показателей. Это достигается за счет использования новых принципов построения структурных схем передатчиков и схемотехнической реализации отдельных их узлов, реализующих цифровые способы формирования, обработки и преобразования колебаний и сигналов, имеющих различные частоты и уровни мощности.
1. Частотные и переходные характеристики систем авторегулирования
Частотная и переходная характеристики замкнутой системы являются показателями качества при гармоническом и скачкообразном воздействиях. Если задающее воздействие гармоническое:
x з (t ) = A coswt ,
то выходной процесс линейной системы тоже гармонический:
y (t ) = AK з (w)cos(wt + jз (w)),
где Кз (w) и jз (w), соответственно, - АЧХ и ФЧХ замкнутой системы.
d(t ) = x з (t ) – y (t ) = A coswt – AK з (w)cos(wt + jз (w))
будет равна нулю только при Кз (w) = 1 и jз (w) = 0. Это требование к идеальной частотной характеристике замкнутой системы. Если все составляющие спектра задающего воздействия попадают в область частот, где частотная характеристика идеальна, то воздействие отрабатывается без ошибки. В противном случае возникает динамическая ошибка.Для оценки качества регулирования по АЧХ замкнутой системы используется показатель колебательности М = К макс /К з (0) (см. рис. 1). Обычно величина показателя колебательности меньше 2.
![]()
Рис.1
![]()
Так как АЧХ будет близка к 1, если К р (w)>>1, независимо от вида частотной характеристики разомкнутой системы в этой области частот.
Для примера рассмотрим системы авторегулирования разного типа: статическую и астатические первого и второго порядка, передаточные функции которых описываются выражениями:
![]() ,
,
![]() ,
, ![]() .(1)
.(1)
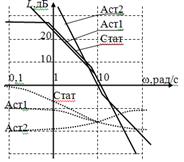
Рис.
Их логарифмические амплитудные характеристики, как видно из рис. 2, значительно отличаются в области нижних и верхних частот. Однако если запасы устойчивости в этих системах одинаковы, то различие в амплитудно-частотных характеристиках замкнутых систем невелико (см. рис. 3). Запас устойчивости по фазе для каждой из этих систем определяется выражениями:
Δφ 1 = 180 – arctg10ωср T 1 – arctgωср Т 1 ,
Δφ 2 = 90 – arctgωср T 2 , (2)
Δφ 3 = arctgωср Т 3 .
По форме АЧХ можно судить о переходной характеристике системы. Так, если АЧХ будет монотонной, то и переходная характеристика монотонна, если в АЧХ будет подъем в области верхних частот, то переходная характеристика будет колебательной.
Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4).

Рис.
Обычно используются следующие числовые параметры переходной характеристики:
время достижения первого максимума tm ,
--> ЧИТАТЬ ПОЛНОСТЬЮ <--