Реферат: Числа Фибоначчи и золотое сечение в живом

х 1-х (1.1)

откуда х2=1-х (1.2)

положительным корнем(1.1) являются _-1_+_√_5_

2

так что отношения в пропорции (1.1) равны

_1_ = ___2___ = ___2(1+√5)__ = _1+√5_ = а

х -1+√ 5 (-1+√5)(1+√5) 2

каждое такое деление (точкой С1) называется делением в среднем и крайнем отношении. Его часто называют также золотым делением или золотым пропорцией (сечением).

Если взять отрицательный корень этого уравнения, то делящая точка С2 окажется вне отрезка АВ (такое деление в геометрии называется внешним делением). Как это видно на рисунке. Легко показать, что и здесь мы имеем дело с золотым сечением:

_С2 В_ = _А В_ = а

АВ С2А

2.Фактическое построение точки, делящей отрезок золотым сечение, осуществляется без труда.

Р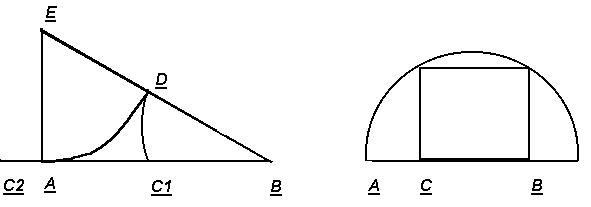
ис. 3 Рис. 4

Пусть АВ=1; востановим из точки перпендикуляр и возьмем точку Е, для которой АЕ=1/2 (рис. 3). Тогда ЕВ = √ 1+(1/2)2 = √5/2.

Проведя из Е, как из центра дугу через А до пересечения с ЕВ в точке D, мы получаем

ВD = _√5-1_

2

Наконец проведя через D дугу с центром в В, мы находим искомую точку С1.точку внешнего деления С2 можно найти из условия АС2 = ВС1.

3.Золотое сечение довольно часто встречается в геометрии, например, для квадрата, вписанного в полукруг (см. рис. 4), точка С делит золотым сечением отрезок АВ.

Сторона правильного десятиугольника (рис.5) вписанного в круг радиуса R, как известно равна

2R sin 360°/2,10 т.е. 2R sin 18°

таким образом,

а 10 =2R _√5-1_ = R _√5-1_ = _R_

4 2 а

И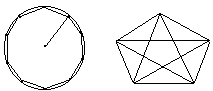

R

А 10

Е

А