Реферат: Дифференциальные и интегральные функции распределения
![]()
Графически эта вероятность выражается отношением площади, лежащей под кривой f (x) в интервале от x1 до x2 к общей площади, ограниченной кривой распределения. Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [− ∞; + ∞] равна единице, т.е. представляет собой достоверное событие. Вероятность этого события называется функцией распределения случайной величины и обозначается F(x). Функцию распределения F(x) иногда называют также интегральной функцией распределения. В терминах интегральной функции распределения имеем
P {x1 ≤ x ≤ x2 }= F (x1 )− F (x2 ),
т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.
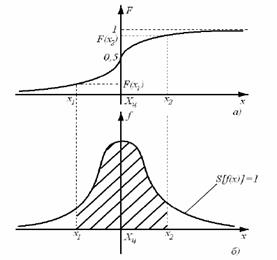
Рис. 3. Интегральная (а) и дифференциальная (б) функции распределения случайной величины
Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина xi в i -м опыте принимает значение, меньшее х. График интегральной функции распределения показан на рис. 3, а. Она имеет следующие свойства:
− неотрицательная, т.е. F(x) ≥ 0;
− неубывающая, т.е. f (x2 ) ≥ F(x1 ), если x2 ≥ x1 ;
− диапазон ее изменения: от 0 до 1, т.е. F(−∞) = 0; F(+∞) = 1;
− вероятность нахождения случайной величины х в диапазоне от x1 до
x2: P{x1 < x < x2 }= F(x2 ) − F(x1 ).
Запишем функцию распределения через плотность:
![]()
Площадь, ограниченная кривой распределения, лежащая левее точки x (х
– текущая переменная) (рис. 4), отнесенная к общей площади, есть не что иное, как интегральная функция распределения F(x) = P{xi < x}.
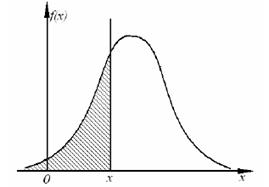
Рис. 4. Кривая плотности распределения вероятностей (дифференциальная функция распределения случайной величины)
Плотность распределения вероятностей f (x) называют
дифференциальной функцией распределения:
![]()
Пример распределения дискретной случайной величины приведен на рис. 5.
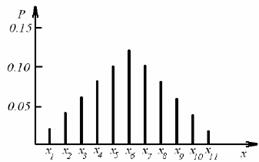
Рис. 5. Распределение дискретной случайной величины
Глава 2. Числовые параметры законов распределения. Центр распределения. Моменты распределений
Функция распределения является самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины специальными параметрами, основными из которых являются:
− центр распределения;
− начальные и центральные моменты и производные от них коэффициенты – математическое ожидание (МО), среднее квадратическое отклонение (СКО), эксцесс, контрэксцесс и коэффициент асимметрии.
Координата центра распределения Xц определяет положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является определение центра по принципу симметрии вероятностей, т.е. нахождение такой точки XM на оси х, слева и справа от которой вероятности появления различных значений случайных погрешностей равны между собой и составляют P1 = P2 = 0,5: