Реферат: Дифференциальные уравнения гиперболического типа

Вводя новые переменные

, ,

уравнение колебания струны преобразуем к виду:

. (4)

Найдем общий интеграл последнего уравнения. Очевидно, для всякого решения уравнения (4)

,

где - некоторая функция только переменного . Интегрируя это равенство по при фиксированном , получим

, (5)

где и являются функциями только переменных и .Обратно, каковы бы ни были дважды дифференцируемые функции и , функция , определяемая формулой (5), представляет собой решение уравнения (4). Так как всякое решение уравнения (4)может быть представлено в виде (5) при соответствующем выборе и , то формула (5) является общим интегралом этого уравнения. Следовательно, функция

(6)

является общим интегралом уравнения (2).

Допустим, что решение рассматриваемой задачи существует; тогда оно дается формулой (6). Определим функции и таким образом, чтобы удовлетворялись начальные условия:

(7)

. (8)

Интегрируя второе равенство, получим:

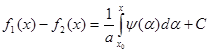
где и C – постоянные. Из равенства

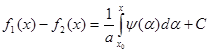
находим:

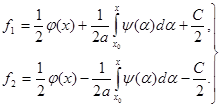(9)

Таким образом, мы определили функции и через заданные функции и , причем равенства (9) должны иметь место для любого значения аргумента. Подставляя в (6) найденные значения и , получим:

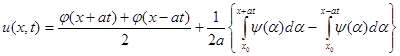
или

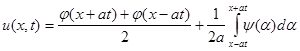, (10)

Формулу (10), называемую формулой Даламбера, мы получили, предполагая существование решения поставленной задачи. Эта формула доказывает единственность решения. В самом деле, если бы существовало второе решение задачи (2) – (3), то оно представлялось бы формулой (10) и совпадало бы с первым решением.

Нетрудно проверить, что формула (10) удовлетворяет (в предположении двукратной дифференцируемости функции и однократной дифференцируемости функции ) уравнению и начальным условиям. Таким образом, изложенный метод доказывает как единственность, так и существование решения поставленной задачи.

2.2.2.Физический интерпретация.

Функция , определяемая формулой (10), представляет собой процесс распространения начального отклонения и начальной скорости. Если фиксировать , то функция дает профиль струны в момент , фиксируя , получим функцию , дающую процесс движения точки . Предположим, что наблюдатель, находившийся в точке x=0 в момент t=0, движется со скоростью a в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая , . В этой подвижной системе координат функция будет определятся формулой и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция представляет неизменный профиль f(x), перемещающийся вправо (в положительном направлении оси x) со скоростью a (распространяющуюся или бегущую волну). Функция f(x+at) представляет, очевидно, волну, распространяющуюся налево (в отрицательном направлении оси x) со скоростью a. Таким образом, общее решение (10) задачи Коши для бесконечной струны есть суперпозиция двух волн , одна из которых распространяется направо со скоростью a, а вторая – налево с той же скоростью. При этом