Реферат: Дифференциальные уравнения гиперболического типа

- момент инерции прямоугольного сечения относительно своей горизонтальной оси. Обозначим через M(x) момент, действующих на правую часть стержня в каждом сечении. В сечении x+dx, очевидно, действует момент сил, равный –(M+dM).

Избыточный момент –dM уравновешивается моментом тангенциальных сил

.

Отсюда в силу равенства (2) получаем величину тангенциальной силы

. (3)

Приравняв действующую на элемент результирующую силу

произведению массы элемента на ускорение

,

где - плотность стержня, S – площадь поперечного сечения (при этом мы пренебрегаем вращательным движением при изгибе), получаем уравнение поперечных колебаний стержня

(). (1)

Граничными условиями для заделанного конца x=0 являются неподвижность стержня и горизонтальность касательной

, . (4)

На свободном конце должны равняться нулю изгибающий момент (2) и тангенциальная сила (3), откуда следует, что

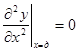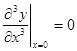, . (5)

Для того чтобы полностью определить движения стержня, нужно еще задать начальные условия – начальное отклонение и начальную скорость

, (). (6)

Таким образом, задача сводится к решению уравнения (1) с граничными условиями (4), (5) и с начальными условиями (6).

Будем решать задачу методом разделения переменных, полагая

y=Y(x)T(t). (7)

Подставляя предлагаемую форму решения в (1), имеем:

.

Для функции Y(x) получаем задачу о собственных значениях

, (8)

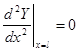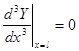, , , . (9)

Общее решение уравнения (8) представляется в виде

.

Из условий Y(0)=0, Y’(0)=0 находим C=-A, D=-B. Отсюда следует, что