Реферат: Дифракція світла

Нехай на досить довгу вузьку прямокутну щілину шириною b перпендикулярно до неї падає плоска світлова хвиля. Розмістимо за щілиною збірну лінзу, а у фокальній площині екран для спостережень результатів дифракції (рис. 3).

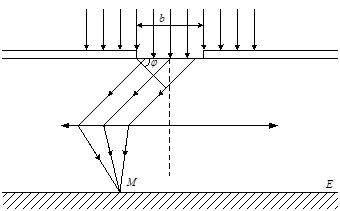
Рис. 3

Щілину шириною b ділять на N вузьких смуг шириною

(9)

де b – ширина щілини; N – число смуг на які поділено щілину; – ширина однієї смуги.

Оптична різниця ходу двох променів від однієї смуги шириною буде дорівнювати

. (10)

Оптична різниця ходу зв’язана з оптичною різницею фаз співвідношення

(11)

де – хвильове число; – кут дифракції.

Для знаходження результуючої амплітуди від всіх смуг, яка буде збуджуватися в точці М (рис.3), використаємо формулу результуючої амплітуди при інтерференції багатьох хвиль

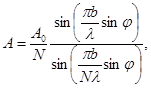(12)

де – амплітуда хвиль від всієї щілини; N – число смуг, на які поділена щілина шириною b ; – кут дифракції.

Розглянемо випадок, коли . У цьому випадку

. (13)

Формула (12) з урахуванням (13) перепишеться

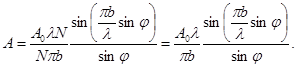(14)

Оскільки інтенсивність світлових хвиль пропорційна , то

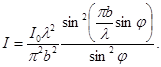(15)

Знайдемо умови мінімуму й максимуму дифракції світлових хвиль, які приходять у точку М (рис.3) від однієї щілини. У точці М інтенсивність світлових хвиль буде дорівнювати нулю, якщо . Це можливо лише у випадку, коли , звідки

(16)

де b – ширина щілини; – кут дифракції; k – порядок максимуму; – довжина хвилі монохроматичного світла.

Умова (16) є умовою мінімуму дифракції від однієї щілини.

У точці М буде спостерігатись максимум дифракції, якщо . Це можливо за умови, коли , звідки

. (17)

Умова (17) є умовою максимуму дифракції від однієї щілини.

Покажемо залежність амплітуди хвиль, які проходять від однієї щілини в точку накладання, від кута дифракції .

а) Якщо підставити в (12) значення кута дифракції , то одержимо невизначеність типу . Для розкривання цієї невизначеності використаємо правило Лопіталя.