1
 K
K
Практический интерес представляют ошибки для каждого из слагаемых полиномиального воздействия. Если воздействие постоянно (xз = =x0), то ошибку называют статической δст; если xз(t) = Vxt, – скоростной δск, а при xз(t)=аxt2/2 – ошибкой по ускорению δуск. Так как эти воздействия имеют конечное количество производных, то ошибки определяются первыми членами ряда:
δст = S0x0,
δск = S0Vxt + S1Vx, (11)
δуск = S0axt2/2 + S1axt + S2ax.
Для расчета этих ошибок надо знать только три первых коэффициента.
На рис. 24 показано, как отрабатываются постоянное и линейное воздействия в статической и астатических системах. Видим, что статическая система обладает наибольшими ошибками. Чем выше порядок астатизма, тем точнее система отрабатывает полиномиальное воздействие.












???. 24
Рассмотрим теперь ошибки при случайных воздействиях. Задающее воздействие описывается медленно меняющимся случайным процессом, спектральная плотностьSxз(ω) которого сосредоточена в области низких частот. Возмущающее воздействие является широкополосным процессом со спектральной плотностью Sxв(ω), и его часто считают белым шумом. Если задающее и возмущающее воздействия некоррелированы, то в соответствии с выражением (10) энергетический спектр динамической ошибки
Sдин(ω) = Sxз(ω)|Кош(jω)|2.
Дисперсия динамической ошибки
 .
.
Дисперсия ошибки по возмущению
 .
.
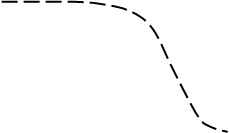
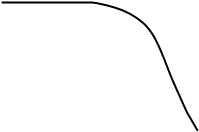
Рассмотрим, как влияет тип системы (статическая или астатическая) на ошибки при случайных воздействиях. На рис. 25,а изображены ЛАХ и ЛФХ разомкнутой системы для трех типов систем, передаточные функции которых приведены в таблице. Эти характеристики различаются лишь в области нижних частот, а в области средних и верхних частот одинаковы. Если коэффициент передачи разомкнутой системы К достаточно большой, то
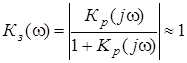
и АЧХ замкнутой системы для всех трех типов будут близки друг к другу (см. рис. 25,б). Следовательно, статическая и астатические системы будут иметь примерно одинаковые ошибки.




























???. 25
Как правило, изменение какого-либо параметра системы (коэффициента передачи К или постоянной времени Т) приводит к противоположному изменению дисперсий динамической ошибки и ошибки по возмущению. Рассмотрим это на примере астатической системы первого порядка.
Допустим, задающее воздействие формируется из белого шума с спектральной плотностью Sз0 пропусканием его через интегрирующую цепь с постоянной времени Tx. Тогда дисперсия задающего воздействия
автоматический регулирование передача
 .
.
Для расчета дисперсии динамической ошибки нужно знать частотную характеристику ошибки Кош(jω):
 .
.
Дисперсия динамической ошибки:
 .
.
Вводя относительные величины α = 1/Txи β = T/Tx и учитывая выражение для дисперсии задающего воздействия, получаем:
 . (12)
. (12)
Видим, что при К = 0 дисперсия динамической ошибки равна дисперсии задающего воздействия. Это объясняется тем, что при К = 0 выходной процесс y(t) = 0 и ошибка становится равной задающему воздействию. С увеличением коэффициента передачи К дисперсия уменьшается и стремится к постоянной величине, равной β. На первый взгляд может показаться, что получен результат, противоречащий здравому смыслу. Ведь с увеличением коэффициента передачи разомкнутой системы расширяется полоса пропускания замкнутой системы, значит, должны лучше отрабатываться высокочастотные составляющие задающего воздействия, и ошибка должна стремиться к нулю. Но никакого противоречия нет. Результат объясним, если учесть форму частотной характеристики ошибки. С увеличением К уменьшается запас устойчивости по фазе и, следовательно, увеличивается подъем АЧХ замкнутой системы в области верхних частот. А так как Кош(jω) = 1 – Кз(jω), то уменьшение спектральной плотности задающего воздействия компенсируется увеличением модуля частотной характеристики ошибки.
Дисперсия ошибки по возмущению при условии, что возмущающее воздействие является белым шумом со спектральной плотностью Sв0, равна:
К-во Просмотров: 275
Бесплатно скачать Реферат: Динамические ошибки в системах авторегулирования
![]() K
K


![]() .
.![]() .
.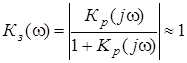






 .
. .
. .
. . (12)
. (12)