Реферат: Динамическое программирование и вариационное исчисление

Т.е. получим δJ=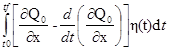≡ 0.

По основной лемме вариационного исчисления: если есть функции r(t) и g(t), при t[t0,tf], причём

g(t0)=g(tf)=0 и =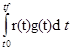≡ 0 , то r(t) ≡ 0 для любых t[t0,tf].

Значит для

δJ=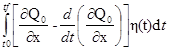≡ 0 получим, что 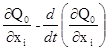≡0, i=1,n.

Полученное уравнение называется уравнением Эйлера (оно выражает 1-е необходимое условие экстремума функционала).

2.3. Трудности, связанные с решением вариационной задачи

При отыскании оптимального управления вариационными методами приходится сталкиваться с трудностями, ряд которых носит принципиальный характер:

1. Вариационные методы дают возможность находить только относительные максимумы и минимумы функционала J(u), тогда как интерес представляет нахождение абсолютного максимума или минимума.

2. Уравнения Эйлера для многих технических задач оказываются нелинейными, что часто не дает возможности получить решение вариационной задачи в явном виде.

3. На значения управляющих сигналов обычно бывают наложены ограничения, делающие невозможным поиск оптимального управления вариационными методами.

Поскольку последнее обстоятельство имело решающее значение для развития новых идей в области оптимального управления, остановимся на нем более подробно.

Обычными ограничениями, накладываемыми на сигналы управления, являются ограничения вида |ui(t)|≤ Mi.

Означающие необходимость ограничения по величине сигналов, подводимых к органам управления. Так, ограниченными являются предельное напряжение, подводимое к якорю электродвигателя, предельный угол поворота руля самолета, предельная температура в камере эрания реактивного двигателя и т.п. При этом получение оптимальных процессов требует, как правило, поддержания сигналов управления на предельных значениях, что соответствует наиболее быстрому и эффективному протеканию процессов в объекте управления. Типичный для этих случаев характер изменения управления u(t) при оптимальном процессе приведен на рис.1.

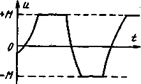
Рис.1. Характерный вид оптимального управляющего сигнала

Однако предельные значения управления u(t) лежат на границах области допустимых управлений U и, следовательно, не являются внутренними точками этой области, для которых только и применимы вариационные

Один из подходов к вычислению оптимальных процессов получил название динамического программирования. Метод динамического программировании дает в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно.

2.4. Метод динамического программирования

2.4.1. Дискретная форма вариационной задачи

Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов, одним из которых является метод динамического программирования. Этот метод дает возможность находить оптимальное уп­равление в многошаговых задачах. Однако он может применяться и для решения вариационных задач, если их представить в дискретной форме.

Воспользовавшись теоремой, сформулируем вариационную задачу в следующем виде: для объекта, описываемого дифференциальным уравнением, x(t)=g(x,u), x(0)=c, найти управление u(t) из области допустимых управления U, которое минимизирует функционал

J(u)= , где Q(x,u)=Q1(x,u)+λH(x,u).

Дискретную форму записи этой задачи получим, если выбор управления u(t) будем производить только в дискретные моменты t=kδ, k=0,n-1, где δ=Т/n, При этом вместо функции x(t) и u(t) будем рассматривать последовательности

xk=x(t)|t=kδ, uk=u(t)|t=kδ.

Заменяя производную x=dx/dt на отношение приращений (xk+1-xk)/δ, вместо дифференциального уравнения получаем уравнение в конечных разностях:

g(xk,uk)

Обычно это уравнение записывают в более удобной форме, разрешая его относительно хk+1: xk+1=xk+ g(xk,uk) δ, k=0,n-1, x0=c.

При этом интеграл

J(u)=

заменится суммой

Jn(u)= ,