Реферат: Динамическое программирование и вариационное исчисление

Теперь задача заключается в выборе таких управлений ui, которые обеспечивают минимальное значение суммы.

Во многих задачах управления оказывается целесообразным считать δ=1. В частности, это удобно делать в тех случаях, когда процесс естественным образом разбивается на отдельные шаги, причем в пределах каждого шага управление u(t) остается неизменным. При этом мы приходим к многошаговому процессу управления, рассмотренному ранее, в котором xk и uk означают состояние объекта и применяемое управление в начале каждого шага.

2.4.2.Рекуррентное соотношение метода динамического программирования

Оптимизация управления n-шагового процесса состоит в том, чтобы найти такую последовательность управлений ui, при которой критерий качества Jn(u) принимает минимальное значение. Это минимальное значение критерия качества управления n-шагового процесса будет зависеть только от начального состояния x0 и его можно обозначать fn(x0). По определению имеем:

fn(x0)=minmin … min [Q(x0,u0)+ Q(x1,u1)+…+ Q(xn-1,un-1)].

Заметим, что первое слагаемое этого выражения Q(x0,u0) зависит только от управления u0, тогда как остальные слагаемые зависят как от u0, так и от управлений на других шагах. Так, Q(x1,u1) зависит от u1, но оно зависит и от u0, так как x1 =T(x0,u0). Аналогично обстоит дело и с остальными слагаемыми. Поэтому выражение можно записать в виде

fn(x0)=min {Q(x0,u0)+ min … min [Q(x1,u1)+…+ Q(xn-1,un-1)]}.

Заметим далее, что выражение min … min [Q(x1,u1)+…+ Q(xn-1,un-1)] представляет собой минимальное значение критерия качествa управления (n-1)-шагового процесса, имеющего начальное состояние х1. В соответствии с определением эту величину можем обозначить через fn-1(x1). Таким образом, получаем: fn(x0)=min {Q(x0,u0)+ fn-1(x1)}.

Эти рассуждения можно повторить, если рассмотреть (n-1)-шаговый процесс, начинающийся с начального состояния x1. Минимальное значение критерия качества управления для этого случая fn-1(x1)=min {Q(x1,u1)+ fn-2(x2)}.

Продолжая эти рассуждения, получаем аналогичное выражение для (n -k) -шагового процесса, начинающегося с состояния xk:

fn-k(xk)=min {Q(xk,uk)+ fn-(k+1)(xk+1)}.

Последнее уравнение, называемое часто уравнением Беллмана, представляет собой рекуррентное соотношение, позволяющее последовательно определять оптимальное управление на каждом шаге управляемого процесса.

Сама идея оптимизации управления на каждом шаге отдельно, если трудно оптимизировать сразу весь про­цесс в целом, не является оригинальной и широко используется на практике. Однако при этом часто не при­нимают во внимание, что оптимизация каждого шага еще не означает оптимизацию всего процесса в целом.

Особенностью метода динамического программирования является то, что оно совмещает простоту решения задачи оптимизации управления на отдельном шаге с дальновидностью, заключающейся в учете самых отда­ленных последствий этого шага.

В методе динамического программирования выбор управления на отдельном шаге производится не с точки зрения интересов данного шага, выражающихся в минимизации потерь на данном шаге, т.е. величины Q(xk,uk), а с точки зрения интересов всего процесса в целом, выражающихся в минимизации суммарных потерь Q(xk,uk)+ fn-(k+1)(xk+1) на всех последующих шагах. Отсюда следует основное свойство оптимального процесса, заключающееся в том, что каковы бы ни были начальное состояние и начальное управление, последующие управления должны быть оптимальными относительно состояния, являющегося результатом применения первого управления.

Из основного свойства оптимального управления следует, что оптимизация управления для произвольной стадии многошагового процесса заключается в выборе только последующих управлений. Поэтому бывает удобно учитывать не те шаги, которые уже были пройдены, а те, которые осталось проделать, для того чтобы привести процесс в конечное состояние.

2.5. Вариационная задача условной минимизации для условий в виде равенств

Рассматриваемая задача состоит в определении управляющих воздействий u(t) минимизирующих (или максимизирую­щих) показатель качества J.

Объект управления описы­вается уравнениями: x=q(x,u,t),

y=g(x,t).

Составляющие q, g предполагаются непрерывными по х и u и не­прерывно дифференцируемыми по х. Объект управления предполагается управляемым и наблюдаемым, т.е. все переменные состояния доступны измерению и возбуждается любое из состояний управляемого объекта.

Если переменные функции не являются независимыми, а подчинены ограничениям типа равенств, т. е. f(x)=0, то необходимые условия экстремума определяются методом множителей Лагранжа.

Пусть целевая функция имеет вид:

J=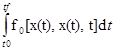-min, при условиях x(t0)=x0 , x(tf)=xf , t[t0,tf], x(t)Rn,

при ограничениях fi(x(t),x(t),t)=0, i=1,m.

Задача решается методом множителей Лагранжа:

запишем лагранжиан

J=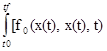+λi(t)fi(x(t),x(t),t)] dt-min по x(t), λ(t).

Запишем более в компактном виде:

J=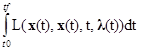=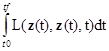-min по z(t), где z(t)=.

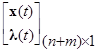Первым необходимым условием экстремума функционала J является δJ=0.