Реферат: Дискретная математика 3

в) Первая цифра принадлежит {1, 2, 3, 4, 5}. Четвертая цифра принадлежит {1, 3, 5}. Вторая и третья цифра принадлежит {0, 1, 2, 3, 4, 5}. Всего чисел: 5∙6∙6∙3=540.

§2.Размещения с повторениями.

Имеются предметы n различных видов а₁ , а₂ , …, а_{n .} Из них составляют всевозможные расстановки длины k. ( Например, а₂ а₁ а₃ а₃ а₄ – расстановка длины 5). Такие расстановки называются размещениями с повторениями из n по k элементов.

Найдем общее число расстановок, среди которых две расстановки считаются различными, если они отличаются друг от друга или видом входящих в них предметов, или порядком этих предметов.

При составлении указанных расстановок длины k на каждое место можно поставить предмет любого вида. Рассмотрим множества Х₁ =Х₂ =…=Х_k ={a₁ , a₂ , …, a_n }. Тогда все размещения с повторениями составят множество Х₁ ´Х₂ ´…´Х_k . По правилу прямого произведения получаем, что общее число размещений с повторениями из n элементов по k местам равно |Х₁ ´Х₂ ´…´Х_k |=n^k .

§3. Размещения без повторений.

Имеются n различных предметов а₁ , а₂ , а₃ , …, а_n . Сколько из них можно составить расстановок длины k. Две расстановки считаются различными, если они отличаются видом входящих в них элементов или порядком их в расстановке. Такие расстановки называются размещенные без повторений, а их число обозначают .

При составлении данных расстановок на первое место можно поставить любой из имеющихся n предметов. На второе место можно поставить только любой из n-1 оставшихся предметов. И наконец, на k-ое место – любой из n-k+1 оставшихся предметов. Таким образом, по правилу прямого произведения =n(n-1)(n-2)∙…∙(n-k+1)=.

Пример. В соревнованиях участвуют 17 команд. Сколькими способами могут быть распределены три призовые места?

Решение. Первое место, то есть золотая медаль, может получить любая из 17 команд так как одна команда не может сразу получить две медали, то серебренная медаль уже может получить любая команда из 16 оставшихся. И наконец, бронзовую медаль – любая из 15 оставшихся. Итак, тройку призеров можно выбрать А=17∙16∙15=4080. Или по формуле:

А=15∙16∙17=4080.

§4. Перестановки.

При составлении размещений без повторений из n по k мы получаем расстановки, отличающиеся друг от друга либо составом, либо порядком элементов. Но если брать расстановки, которые включают все n элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие расстановки называются перестановками из n элементов, а их число обозначается Р_n . P_n =A=n!

Пример.

1) |S₃ |=P₃ =3!=6

|S₄ |=P₄ =4!=24

2) Сколькими способами можно расположить на шахматной доске 8 ладей, чтобы они «не били» друг друга?

Решение. Условие «не могли бить» означает, что на каждой горизонтали и вертикали может стоять лишь одна ладья. Ввиду этого, каждому расположению ладей на доске соответствует перестановка π=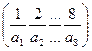. Верхняя строка – это номера горизонталей, нижняя – вертикалей.

а₁ – номер вертикали, в которой стоит ладья из первой горизонтали,

а₂ – номер вертикали, в которой стоит ладья из второй горизонтали, и т.д.

Среди чисел а₁ а₂ …а₈ нет ни одной пары равных, иначе две ладьи попали бы в одну вертикаль. Согласно, расположению ладей соответствует определенная перестановка чисел 1, …, 8 и наоборот, каждой перестановке чисел 1, …, 8 соответствует такое расположение ладей на шахматной доске, при котором они «не бьют друг друга»

Всего таких перестановок Р₈ =8!=40320.

§5. Сочетания.

В тех случаях, когда нас не интересует порядок элементов в расстановке, а интересует лишь ее состав, то говорят о сочетаниях.

Сочетаниями из n различных элементов по k местам называют все возможные расстановки длины k, образованные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов.

# 123 и 132 – одинаковые сочетания.

Общее число сочетаний обозначают С. Определим это число

# Число сочетаний из 5 элементов по 3.

1, 2, 3, 4, 5.

123 134 234 345