Реферат: Дискретная математика 3

K(x)⋅U(x)=С(x), где U(x)=

С(х)=(1-5x+6x² )(u₀ +u₁ x+u₂ x² +…)=

=u₀ +u₁ x+u₂ x² +…-5u₀ x-5u₁ x² -5u₂ x³ -…+6u₀ x² +6u₁ x³ +6u₂ x⁴ +…=

=u₀ +(u₁ -5u₀ )x+(u₂ -5u₁ +6u₀ )x² +(u₃ -5u₂ +6u₁ )x³ +…

Но u₂ =5u₁ -6u₀ , u₃ =5u₂ -6u₁ и так далее. Следовательно,

С(х)=u₀ +(u₁ -5u₀ )x=1-4x.

Характеристическим полиномом будет F(x)=x² -5x+6=(x-2)(x-3).

Отсюда следует, что U(x)==.

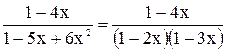С помощью неопределенных коэффициентов разложим последнюю дробь в сумму дробей:

===.

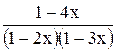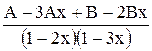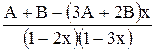Следовательно, 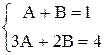Þ.

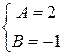Тогда U(x)=, но =, и таким образом, и .

Итак, U(x)===.

Получаем, что u_k =2^{k +1} -3^k .

§10. Неоднородные линейные рекуррентные соотношения.

Неоднородное линейное рекуррентное соотношение имеет вид:

u_n+r =С₁ u_n+r-1 +С₂ u_n+r-2 +…+С_r u_n +b_n (1)

где величина b_n в общем случае является функцией от n. Общее решение соотношения (1) представляет собой сумму частного решения неоднородного уравнения (1) (то есть любого решения, которое ему удовлетворяет) и общего решения соответствующего ему однородного соотношения (1).

Общих способов определения частного решения нет, однако для некоторых значений b_n существуют стандартные приемы определения u_n .

Пример. Найти {u_n }, если u_n+1 =u_n +(n+1) и u₀ =1.

Решение. Умножив левую и правую части рекуррентного соотношения на хⁿ , получим:

u_n+1 xⁿ =u_n xⁿ +(n+1)xⁿ .

Суммирование последнего уравнения для всех n дает:

.

Воспользуемся свойствами операций с производящими функциями:

=U(x) – по определению,

====,

= – см. табл. §9.

Итак, получаем =U(x)+.

Учитывая, что u₀ =1, запишем:

U(x)-1=х×U(x)+,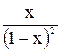

U(x)-x×U(x)=1+,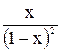

U(x)×(1-x)=,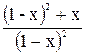

U(x)==.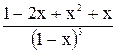

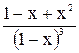Из таблицы следует 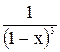== (так как ).

Тогда U(x)=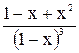=(1-x+x² ) . Но U(x)=. Сравнивая коэффициенты при xⁿ , заключаем, что

u_n ==-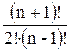+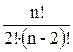= ==(n² +3n+2-n² -n+n² -n)=(n² +n+2).