Остальные рефераты / Реферат: Дискретная математика 3

Реферат: Дискретная математика 3

Для неоднородного линейного рекуррентного соотношения вида

u_n+2 +p×u_n+1 +q×u_n =αn+β, (2)

где α, β, p, q – данные числа, справедливы следующие утверждения:

1) если х₀ =1 не является корнем многочлена х² +px+q, то частным решением рекуррентного соотношения (2) является последовательность u=аn+b;

2) если х₀ =1 является простым корнем многочлена х² +px+q, частное решение рекуррентного соотношения (2) может быть найдено в виде u=n(аn+b);

3) если х₀ =1 является кратным корнем многочлена х² +px+q, частное решение рекуррентного соотношения (2) может быть найдено в виде u=n² (аn+b).

Найдем значения а и b в каждом из перечисленных случаев.

1) u=аn+b, u=а(n+1)+b, u=а(n+2)+b.

Подставляя эти значения в выражение (2). получим

an+2a+b+pan+pa+pb+qan+qb=αn+β,

(a+pa+qa)n+2a+b+pa+pb+qb=αn+β.

Следовательно, 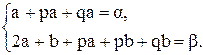Так как х₀ =1 не является корнем многочлена х² +px+q, то 1+p+q¹0, и тогда имеем

а=,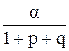

b=.

2) u=n(аn+b), u=(n+1)(an+a+b), u=(n+2)(an+2a+b).

Подставляем эти значения в (2):

(n+2)(an+2a+b)+p(n+1)(an+a+b)+qn(an+b)=αn+β,

an² +2an+nb+2an+4a+2b+pan² +pan+pbn+pan+pa+pb+qan² +qbn=αn+β,

(a+pa+qa)n² +(4a+b+2pa+pb+qb)n+(4a+2b+pa+pb)=αn+β.

Тогда

1+p+q=0, так как х₀ =1 является простым корнем многочлена х² +px+q. Значит,

a(4+2p)=α Þ a=.

b==.

3) u=n² (аn+b), u=(n+1)² (an+a+b), u=(n+2)² (an+2a+b).

(n+2)² (an+2a+b)+p(n+1)² (an+a+b)+qn² (an+b)=αn+β,

Заметим, что, если х₀ =1 является кратным корнем уравнения х² +px+q=0, то уравнение имеет вид (х-1)² =0 или х² -2х+1=0, то есть р=-2 и q=1.

(n+2)² (an+2a+b)-2(n+1)² (an+a+b)+n² (an+b)=αn+β,

(n² +4n+4)(an+2a+b)-2(n² +2n+1)(an+a+b)+an³ +bn² =αn+β,

an³ +2an² +bn² +4an² +8an+4bn+4an+8a+4b-2an³ -2an² -2bn² -4an² -4an-4bn-2an-2a- -2b+an³ +bn² =αn+β,

n³ (a-2a+a)+n² (2a+b+4a-2a-2b-4a+b)+n(8a+4b+4a-4a-4b-2a)+(8a+4b-2a-2b)=αn+β.

Þ a=, b=.

Пример. Решить рекуррентное соотношение u_n ₊₂ -3u_n ₊₁ +2u_n =n, u₀ =1, u₁ =1.

Решение. p=-3, q=2, α=1, β=0.

Соответствующее уравнение х² -3х+2=0 или (х-1)(х-2)=0. х₀ =1 является простым корнем многочлена, следовательно, частное решение будет иметь вид u=аn+b, где а==- и b==-.