Реферат: Дискретно-аналоговое представление
где ![]() - интерполирующая (восстанавливающая, синтезирующая) функция. Функция
- интерполирующая (восстанавливающая, синтезирующая) функция. Функция
![]() , (5)
, (5)
т.е. ![]() есть функция с началом отсчета в точкемер выборки первичного сигнала. Суммирование в выражении (4) ведется по всем выборкам, участвующим в обработке. Определение вида функции
есть функция с началом отсчета в точкемер выборки первичного сигнала. Суммирование в выражении (4) ведется по всем выборкам, участвующим в обработке. Определение вида функции ![]() составляет сущность задачи выбора способа интерполяционной обработки.
составляет сущность задачи выбора способа интерполяционной обработки.
На точность функции восстановления функции ![]() влияют следующие факторы:
влияют следующие факторы:
-шумы интерполяции;
-шумы радиолинии;
-погрешности системы.
В дальнейшем будем учитывать только ошибку за счет интерполяции. Т.е. выборки будут считаться точными, а шумы отсутствующими. Тогда выражение для оценки первичного сигнала будет иметь следующий вид:
![]() . (6)
. (6)
Ошибка интерполяционной обработки в этом случае равна:
![]() . (7)
. (7)
При этом оценка ![]() должна быть получена на некотором интервале интерполяции
должна быть получена на некотором интервале интерполяции ![]() с учетом выборок, расположенных на конечном интервале обработки
с учетом выборок, расположенных на конечном интервале обработки ![]() . Интервал обработки
. Интервал обработки ![]() должен последовательно перемещаться в пределах интервала наблюдения
должен последовательно перемещаться в пределах интервала наблюдения ![]() (рисунок 2).
(рисунок 2).
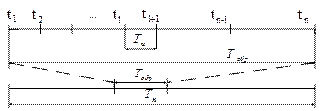
Рисунок 2
Таким образом, функция ![]() должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции
должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции ![]() , путем использования выборок в моменты времени
, путем использования выборок в моменты времени ![]() .
.![]() Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала
Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала ![]() , моментами времени
, моментами времени ![]() и
и ![]() . Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.
. Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.
Теоретически необходимо учитывать все отсчеты ![]() на интервале наблюдения
на интервале наблюдения ![]() , т.е. полагать
, т.е. полагать ![]() =
= ![]() . Но при этом результаты интерполяции могут быть получены спустя время
. Но при этом результаты интерполяции могут быть получены спустя время ![]() , и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции
, и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции ![]() уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией
уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией ![]() на интервале интерполяции
на интервале интерполяции ![]() , с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.
, с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.
2. Физическая трактовка процессов интерполяции сигналов
Основное математическое соотношение интерполяционной обработки:
![]() , (8)
, (8)
можно проиллюстрировать следующим образом (рисунок 3).
В качестве интерполяционной функции в этом примере используется функция ![]() . Интервалы интерполяции
. Интервалы интерполяции![]() и обработки
и обработки ![]() должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
![]() . (9)
. (9)
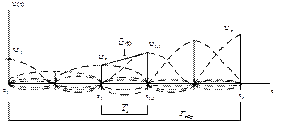
Рисунок 3
Для доказательства этого утверждения обозначим сигнал на входе и выходе линейного фильтра через ![]() и
и ![]() (рисунок 4):
(рисунок 4):
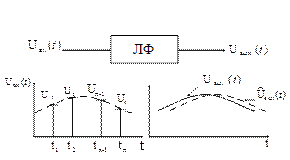
Рисунок 4
Представим сигнал на входе линейного фильтра в виде последовательности кратковременных импульсов, площадь которых равна соответствующим выборкам
![]() . (10)
. (10)