Реферат: Дисциплины обслуживания. Модель с приоритетами. Дисциплины обслуживания с приоритетами, зависящими от времени
Дисциплины обслуживания. Модель с приоритетами.
Дисциплина обслуживания – это способ определения того, какое требование в очереди должно обслуживаться следующим. Решение может основываться на одной из приведенных ниже характеристик или на их совокупности:
1) мера, определяемая относительным временем поступления рассматриваемого требования в очередь;
2) мера требуемого или полученного до сих пор времени обслуживания;
3) функция, определяющая принадлежность требования к той или иной группе.
Примерами дисциплин обслуживания являются постоянно используемая модель «первый пришел - первый обслужен» (FCFS-first came-first served), называемая в русскоязычной литературе «дисциплина обслуживания в порядке поступления»-ОПП. Приведем здесь список некоторых типичных дисциплин обслуживания.
ОПП-обслуживание в порядке поступления (FCFS);
ООП – обслуживание в обратном порядке, т.е. последнее поступившее требование обслуживается первым (LCFS);
ПК – первоочередное обслуживание требований с кратчайшей длительностью обслуживания (SPT/SJE);
ПКД – первоочередное обслуживание требований с кратчайшей длительностью дообслуживания (SRPT);
ПКС – первоочередное обслуживание требований с кратчайшей средней длительностью обслуживания (SEPT);
ПКСД – первоочередное обслуживание требований с кратчайшей средней длительностью дообслуживания (SERPT);
ПКОВ – первоочередное обслуживание требований с кратчайшим обязательным временем (SIPT).
Если сравнивать эти дисциплины по среднему времени ожидания попарно, и обозначать тот факт, что среднее время ожидания для дисциплины D1 ,больше или равно среднему времени ожидания для дисциплины D2 следующим образом: D1 ®D2 , то можно построить следующую диаграмму
ПО ® ОПП ® ПК ® ПКД
¯
¯® ОП ®®®®
Итак, основным предметом анализа различных дисциплин обслуживания будем считать расчет среднего времени ожидания требования в очереди или среднего времени пребывания в системе.
Предположим, что требования принадлежат одному из P различных приоритетных классов, обозначаемых индексом p =1,2,3…P . Каждому требованию, находящемуся в системе в момент времени t ставится в соответствие значение некоторой приоритетной функции qp (t). Чем больше значение этой функции, тем выше приоритет требования. Всякий раз, когда принимается решение для выбора требования на обслуживание, выбор делается в пользу требования с наибольшим значением приоритетной функции. В простейшем случае в качестве приоритетной функции выбирается просто значение p . В этом случае приоритет требования тем больше, чем больший номер класса принадлежности оно имеет. Рассмотрим достаточно общую модель, основанную на системе M/G/1. Предположим, что требования из приоритетного класса p образуют пуассоновский поток с интенсивностью l p требований в секунду. Время обслуживания каждого требования из этого класса выбирается независимо в соответствие с распределением с плотностью вероятности bp (x) со средним значением
![]() .
.
Введем следующие определения
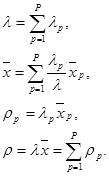
Здесь r интерпретируется как доля времени, в течение которого сервер занят (r <1), а каждый из парциальных коэффициентов r p – как доля времени, в течение которого сервер занят обслуживанием заявок из приоритетного класса с номером p .
Если требование в процессе обслуживания может быть удалено из сервера и возвращено в очередь при поступлении требования с более высоким приоритетом, то говорят, что система работает с абсолютным приоритетом, если обслуживание любого требования, находящегося в сервере не может быть прервано, то говорят что СМО работает с относительным приоритетом.
Основная модель расчета среднего времени ожидания
Будем использовать далее следующие обозначения для среднего значения времени ожидания в очереди требований из приоритетного класса p - Wp , и среднего времени пребывания в системе для требований этого класса - Tp :
![]() .
.
Основное внимание будем уделять системам с относительным приоритетом. Рассмотрим процесс с момента поступления некоторого требования из приоритетного класса p . Будем далее называть это требование меченым. Первая составляющая времени ожидания для меченого требования связана с требованием, которое оно застает в сервере. Эта составляющая равна остаточному времени обслуживания другого требования. Обозначим теперь и будем использовать это обозначение и далее, среднюю задержку меченого требования, связанную с наличием другого требования на обслуживании W0 . Зная распределение времени между соседними поступлениями входных требований для каждого приоритетного класса, можно всегда вычислить эту величину. В нашем предположении пуассоновского закона для потока заявок каждого класса можно записать
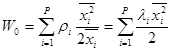 .
.
Вторая составляющая времени ожидания для меченого требования определяется тем, что перед меченым требованием обслуживаются другие требования, которые меченое требование застало в очереди. Обозначим далее число требований из класса i , которое застало в очереди меченое требование (из класса p ) и которые обслуживаются перед ним Nip . Среднее значение этого числа будет определять величину среднего значения этой составляющей задержки
--> ЧИТАТЬ ПОЛНОСТЬЮ <--