Реферат: Двухкритериальные модели управления портфельными инвестициями с учетом риска
где ![]() - число лотов, в которые входят ценные бумаги вида i.
- число лотов, в которые входят ценные бумаги вида i.
Задача (1)-(4) является целочисленной задачей линейного программирования (I – множество целых чисел), в которой неравенство (3) задает приемлемый риск портфеля.
Целочисленная модификация модели оптимизации портфеля Г. Марковица, учитывающая ограничения на объемы Vi (i=1,…,n) лотов приобретаемых ценных бумаг с критерием риска, выраженным через дисперсию портфеля, соответствует классической постановке задачи.
Обозначим долю финансовых ресурсов, затраченных на приобретение лота Vi , через ![]() . Тогда модификация модели Марковица с критерием на минимум риска с учетом целочисленных переменных может быть представлена в следующем виде:
. Тогда модификация модели Марковица с критерием на минимум риска с учетом целочисленных переменных может быть представлена в следующем виде:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() ;
; ![]() (8)
(8)
где ![]() - множество лотов, в которые входят ценные бумаги вида i;
- множество лотов, в которые входят ценные бумаги вида i;
ΔF задает минимально необходимый прирост инвестиционных ресурсов, определяемый инвестором при реализации активов портфеля в момент времени t=T. Значения covij вычисляются как попарные ковариации актива i и актива j (i=1,…,n; j=1,…n; i≠j), вычисляемые на основе вероятностного распределения доходности этих активов.
В работе предложен метод ветвей и границ для решения задач (1)-(4) и (5)-(8), заключающийся в вычислении верхней и нижней оценки решения оптимизационной задачи на первом этапе и дальнейшем анализе формируемых допустимых портфелей с использованием результатов эффективности вычисления так называемых текущих верхних (текущих нижних) оценок. Неудовлетворительное значение этих оценок в процессе формирования рассматриваемого варианта допустимого портфеля прерывает дальнейший анализ его эффективности, что позволяет существенно сократить полный перебор всех вариантов.
В работе рассмотрены подходы к формированию инвестиционного портфеля с критериями на максимум ожидаемой доходности и ограничениям на уровень риска с использованием авторской модификации целочисленной модели Марковица. С учетом использованных ранее обозначений задач (4) - (8), эта модификация может быть представлена в следующем виде:
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() ;
; ![]() (12)
(12)
где R задает верхнюю границу риска портфеля.
В работе предлагается метода ветвей и границ для решения задачи (9)-(12), основанный на вычислении текущих оценок целевой функции при формировании очередного варианта портфеля ценных бумаг. В качестве верхней оценки выбирается значение целевой функции (9) при ограничениях (11) и (12), то есть ограничение (10) не учитывается. В качестве нижней оценки выбирается значение целевой функции задачи (9)-(12) на сформированном допустимом целочисленном портфеле. Вычисление верхней и нижней оценок ожидаемой доходности оптимального портфеля позволяет при анализе всех возможных вариантов его формирования отбраковать все неэффективные портфели.
В диссертации представлено несколько практических примеров расчета оптимальных портфелей ценных бумаг с использованием целочисленной модели (1)-(4), базирующейся на использовании коэффициентов риска (b i ) 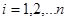 , рассчитанных на основе данных о котировках ценных бумаг, представленных Российской Торговой Системой. Этот коэффициент риска рассчитывается относительно индекса РТС. На практике допустимо заменять «бету» относительно рыночного портфеля (согласно САРМ) на «бету», рассчитанную относительно рыночного индекса, в связи с тем, что точно определить структуру рыночного портфеля, состоящего из всех акций обращающихся на рынке, не удается. Индекс РТС рассчитывается для 68 российских акций. По состоянию на 30 мая 2005 года индекс РТС равнялся 666,79.
, рассчитанных на основе данных о котировках ценных бумаг, представленных Российской Торговой Системой. Этот коэффициент риска рассчитывается относительно индекса РТС. На практике допустимо заменять «бету» относительно рыночного портфеля (согласно САРМ) на «бету», рассчитанную относительно рыночного индекса, в связи с тем, что точно определить структуру рыночного портфеля, состоящего из всех акций обращающихся на рынке, не удается. Индекс РТС рассчитывается для 68 российских акций. По состоянию на 30 мая 2005 года индекс РТС равнялся 666,79.
В работе при формировании портфеля использовались семь видов российских акций, которые входят в 20-ку высоколиквидных ценных бумаг, вращающихся на российском фондовом рынке («Голубые фишки»). Акции выбраны из различных отраслей российской экономики, с тем, чтобы их диверсификация способствовала уменьшению собственного риска портфеля. В их состав вошли:
1) EESR РАО ЕЭС России обыкновенные
2) LKOH ЛУКойл-Холдинг обыкновенные
3) RTKM Ростелеком обыкновенные
4) GUMM ГУМ обыкновенные
5) SNGSP Сургутнефтегаз привилегированные
6) TATN Татнефть обыкновенные
7) YUKO ЮКОС, обыкновенные
Недельный прогноз курса рассматриваемых акций представлен в таблице 1.
Таблица 1. Прогнозируемое изменение курсов акций на 7 июня 2005 года (долл. США за 1 акцию)
| EESR | LKOH | RTKM | GUMM | SNGSP | TATN | YUKO | |
| Текущий курс | 0,26 | 34,6 | 2,1 | 2,3 | 0,54 | 1,76 | 0,5 |
| Прогнозируемый курс | 0,36 | 39,88 | 2,44 | 1,92 | 0,64 | 1,74 | 0,55 |
Выбранные акции продаются лотами в стандартном объеме по 100 акций. В работе рассмотрены различные варианты формирования целочисленных портфелей ценных бумаг, различающиеся по составу акций. Результаты расчетов приведены в таблицах 2-5.
Таблица 2. Оптимальный портфель, состоящий из 4 видов акций, при покупке акций лотами
| EESR | LKOH | RTKM | GUMM | Итого | Лимит | |
| Начальная стоимость 1 акции | 0,28 | 34,6 | 2 | 12,3 | ||
| Будущая стоимость 1 акции | 0,34 | 39,88 | 2,41 | 1,92 | ||
| Количество акций в лоте | 100 | 100 | 100 | 100 | ||
| Коэффициент риска акций | 0,92 | 1,45 | 0,88 | 0,31 | ||
| Инвестиции в акции | 28 | 0 | 200 | 0 | 228 | 2000 |
| Общая доходность по акциям | 6 | 0 | 41 | 0 | 47 | |
| Доля риска акций в портфеле | 0,11 | 0 | 0,77 | 0 | 0,88 | 1,1 |
| Доля акций в портфеле | 1 | 0 | 1 | 0 |