Реферат: Эффективность работы военно-медицинского учреждения

Учитывая, что , перепишем выражение:

, (2.7)

где -коэффициент корреляции между j-ым признаком и r-й главной компонентой, - коэффициент корреляции между r-й и первой главной компонентой, - весовые коэффициенты, которые называются в факторном анализе коэффициентами отображения. Поскольку в методе главных компонент компоненты не коррелированны между собой, можно записать =0 (r¹k), поэтому =. И в общем случае в методе главных компонент можно написать =.

Матрица наблюденных коэффициентов корреляции может быть представлена так:

R =YY ¢, (2.8)

где Y - матрица нормированных значений признаков, Y ¢ - транспонированная матрица.

Коэффициент корреляции характеризует связь между двумя случайными величинами Х_j и Х_r в случае линейной корреляции между ними. Коэффициент корреляции представляет эмпирический первый основной смешанный момент. Для любых признаков и случайных величин , (2.9)

Среднее значение случайной величины Х_j определяется по формуле

, (2.10)

а среднеквадратическое отклонение

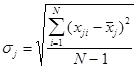. (2.11)

В результате преобразований корреляционной матрицы можно получить y =U L^1/2 f , где L-матрица собственных значений матрицы R , U - матрица из собственных векторов R. Отсюда можно заключить, что искомая матрица А может быть определена как А =U L^1/2 , или, соответственно для столбцов .

Вклад данного вектора а_r в общую дисперсию определится по формуле

. (2.12)

2.2.2. Геометрическая интерпретация метода главных компонент

Геометрической интерпретацией метода главных компонент служит переход к новой системе координат, где осями служат главные компоненты распределения. [3,11].

Рассмотрим простейший двумерный случай. Она представлена на Рис 2.1.

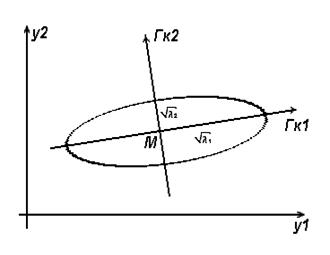
Рис. 2.1. Геометрическая интерпретация метода главных компоент для двумерного случая

2.2.3 Блок схема алгоритма

Блок схема алгоритма метода главных компонент приведена на рисунке 2.2.

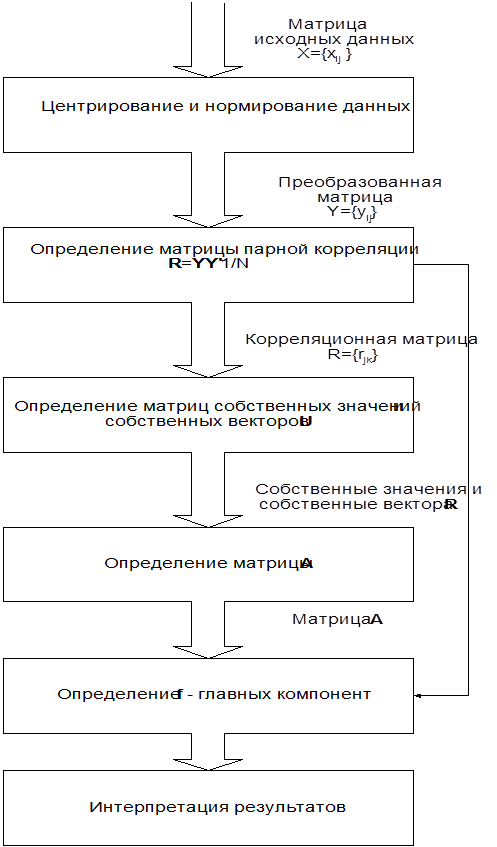
Рис 2.2. Блок схема алгоритма метода главных компонент

2.2.4 Обратная факторная задача

Как было указано выше, каждая главная компонента даёт некую новую общую характеристику всем изучаемым объектам. Причем каждая компонента является функцией особенностей каждого из изучаемых объектов. Часто нас интересует случай, когда нас интересуют качества объектов, связанные с одной или несколькими главными компонентами. Если было бы возможно получить значение компоненты для каждого из рассматриваемых пациентов, то их можно было бы ранжировать и классифицировать по такой важной интегральной особенности, как тяжесть ранения.

Обратимся к модели метода главных компонент. Развернём равенство, для j-ого признака:

(2.13)

Выразим теперь значения главных компонент через значения признаков. Для r-ой компоненты:

. (2.14)