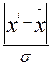Реферат: Экономико статистический анализ эффективности использования основных фондов в сельскохозяйстве

S_{Me -1} – сумма частот домедиальных интервалов;

f_Me – частота медиального интервала.

2) Для характеристики меры рассеяния признака определяют показатели вариации: размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации составит: R=x_max -x_min =582-147=435(г).

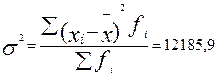Дисперсия определяется по формуле

Среднее квадратическое отклонение признака в ряду распределения составит:

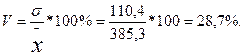Для определения коэффициента вариации используют формулу

Среднесуточный прирост в среднем по хозяйствам составляет 385,3г. Среднесуточный прирост колеблется от 147 до 582г. и размах колебаний составляет 435г. В среднем среднесуточный прирост отклоняется на 110,4г. или на 28,7% от среднего значения. Коэффициент вариации так же показывает, что все хозяйства являются однородными по среднесуточному приросту, т.к. V<33%.

3) 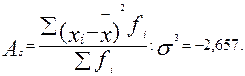Для характеристики формы распределения могут быть использованы коэффициенты асимметрии (A_s ) и эксцесса (Е_s ):

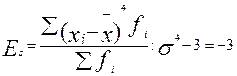Так как A_s <0, распределение имеет левостороннюю асимметрию.

Так как Е_s <0, распределение является низковершинным по сравнению с нормальным.

Для того, чтобы определить, подчиняется ли эмпирическое (исходное) распределение закону нормального распределения, необходимо проверить статистическую гипотезу о существенности различия частот фактического и теоретического (нормального) распределения.

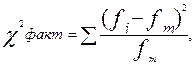Наиболее часто для проверки таких гипотез используют критерий Пирсона (χ² ), фактическое значение которого определяют по формуле

где f_i и f_m – частоты фактического и теоретического распределения.

Теоретические частоты для каждого интервала определяют в следующей последовательности:

1. Для каждого интервала определяют нормированное отклонение (t):

Например, для первого интервала и т.д.

Результаты расчета значений t представлены в таблице 11.

2. 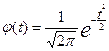Используя математическую таблицу «Значения функции

» , при фактической величине tдля каждого интервала, находят значение функции нормального распределения.

3. Определим теоретические частоты по формуле

где n – число единиц в совокупности;

h - величина интервала.

n=321; h=87; σ=110,4

Таблица 11 – Эмпирическое и теоретическое распределение предприятий по среднесуточному приросту

Срединное значение интервала по среднесуточному приросту,г.	Число хозяйств
xi	fi	t	табличное	fm	-
190,5	2	1,76	0,0848	1	0,25
277,5	4	0,98	0,2468	4	0,00
364,5	7	0,19	0,3918	7	0,00
451,5	3	0,60	0,3332	6	1,15
538,5	5	1,39	0,1518	3	2,46
Итого	21	x	x	21	3,87

4. Подсчитаем сумму теоретических частот и проверим ее равенство фактическому числу единиц, т.е. ∑f_i ∑f_m .

Таким образом, фактическое значение критерия составило:

По математической таблице «Распределение χ² » определяют критическое значение критерия χ² при числе степеней свободы (υ) равном числу интервалов минус единица и выбранном уровне значимости. При υ= 5-1 = 4 и α=0,05