Реферат: Экстремумы функций многих переменных
Кафедра ВЫСШЕЙ МАТЕМАТИКИ
Реферат
На тему : “ Экстремумы функций многих переменных ”
Выполнил :
Студент группы ТЭ-97-1
Мартынов Ф.О.
Проверила :
Преподаватель кафедры
Седых Е.И.
Иркутск 1998
План реферата :
1. Понятие экстремума........................... 2
2. Необходимые условия экстремума.. 3
3. Достаточные условия экстремума... 6
4. Локальные экстремумы.................... 8
5. Условные экстремумы...................... 9
Экстремумы функций многих переменных.
Для начала рассмотрим необходимые условия экстремума функции, также определим понятие экстремума.Начнем с понятия экстремума:
Положим, что имеется некоторая функция с двумя переменными 
Определение : Точка 
называется точкой экстремума (максимума или минимума)
функции 
, если 
есть соответственно наибольшее или наименьшее значение функции 
в некоторой окрестности точки 
.
При этом значение 
называетсяэкстремальным значением функции (соответственно максимальным или минимальным ). Говорят также, что функция 
имеет в точке 
экстремум (или достигает в точке 
экстремума).
Заметим, что в силу определения точка экстремума функции лежит внутри области определения функции, так что функция определена в некоторой (хотя бы и малой) области, содержащей эту точку. Вид поверхностей, изображающих поверхности функций в окрестности точек экстремума показан на рис. 1.
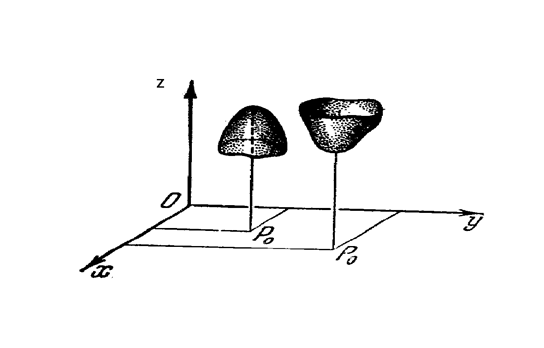
Теперь установим необходимые условия, при которых функция 
достигает в точке 
экстремума; для начала будем рассматривать только дифференцируемые функции.
Необходимый признак экстремума : Если в точке 
дифференцируемая функция 
имеет экстремум, то ее частные производные в этой точке равны
нулю :
, 
.
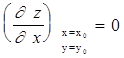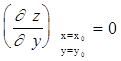Доказательство : Допустим, что функция 
имеет в точке 
экстремум.
Согласно определению экстремума функция 
при постоянном
, как функция одного 
достигает экстремума при 
. Как известно, необходимым условием для этого является обращение в нуль производной от функции 
при 
,
т. е.
.
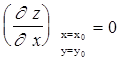Аналогично функция 
при постоянном 
, как функция одного 
, достигает экстремума при 
. Значит,
Что и требовалось доказать.
Точка 
, координаты которой обращают в нуль обе частные производные функции 
, называется стационарной точкой функции 
.
Уравнение касательной плоскости к поверхности 
:
для стационарной точки 
принимает вид 
.
Следовательно, необходимое условие достижения дифференцируемой функцией экстремума в точке геометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.
Для отыскания стационарных точек функции 
нужно приравнять нулю обе ее частные производные
, 
. (*)
и решить полученную систему двух уравнений с двумя неизвестными.
Пример 1 : Найдем стационарные точки функции
Система уравнений (*) имеет вид:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--