Реферат: Экстремумы функций многих переменных

Эти уравнения определяют линию в пространстве. Таким образом задача сводится к отысканию такой точки линии, в которой функция принимает экстремальное значение, причем сравниваются значения функции только в точках рассматриваемой линии.

Метод множителей Лагранжа в этом случае принимается следующим образом: строим вспомогательную функцию

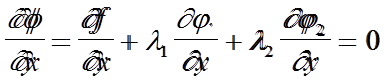
Ф(x, y, z) = f(x, y, z)+l₁ j₁ (x, y, z) +l₂ j₂ (x, y, z), где l₁ и l₂ - новые дополнительные неизвестные, и состовляем систему уравнений для отыскания экстремумов этой функции.

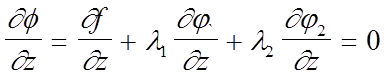
Добавляя сюда два уравнения связи получаем систему уравнений с пятью неизвестными x, y, z, l₁ , l₂ . Искомыми точками условного экстремума могут быть только те, координаты х, у, z которых являются решением этой системы.

Список использованной литературы:

А.Ф. Бермант, И.Г. Абрамович. Краткий курс математического анализа.

Шипачев Учебник высшей математики