Реферат: Электрические цепи постоянного тока

При расчете цепи этим методом составляют систему уравнений по второму закону Кирхгофа для всех независимых контуров. Затем полагают, что в каждом независимом контуре «к» протекает свой контурный ток I_кк условное положительное направление которого совпадает с направлением обхода этого контура. Если ветвь является общей для нескольких контуров, то ток в ней будет равен алгебраической сумме контурных токов, замыкающих эту ветвь.

В общем случае система уравнений для цепи, имеющей и независимых контуров имеет следующий вид:

R₁₁ I₁₁ + R₁₂ I₂₂ + R₁₃ I₃₃ +… + R_1n I_nn = E₁₁ ,

R₂₁ I₁₁ + R₂₂ I₂₂ + R₂₃ I₃₃ + … + R_2n I_nn = E₂₂ , (1.5)

R₃₁ I₁₁ + R₃₂ I₂₂ + R₃₃ I₃₃ + … + R_3n I_nn = E₃₃ ,

…………………………………………...

R_n1 I₁₁ + R_n2 I₂₂ + R_n3 I₃₃ + … + R_nn I_nn = E_nn ,

где E₁₁ , E₂₂ , E₃₃ , … , E_nn – контурные ЭДС, равные алгебраической сумме ЭДС в соответствующих контурах, причем ЭДС считают положительными, если их условные положительные направления совпадают с направлением обхода контура (контурного тока), и отрицательными, если их направления противоположны; R₁₁ , R₂₂ , R₃₃ , … , R_nn — собственные сопротивления тех же контуров, равные сумме сопротивлений всех резисторов, принадлежащих соответствующему контуру; R₁₂ = R₂₁ , R₂₃ = R₃₂ и так далее — взаимные сопротивления контуров, равные сумме сопротивлений резисторов, принадлежащих одновременно двум контурам, номера которых указаны в индексе. При этом взаимные сопротивления надо принимать: а) положительными, если контурные токи в них направлены одинаково; б) отрицательными, если они направлены встречно; в) равными нулю, в) равными нулю, если контуры не имеют общей ветви.

Число независимых контуров, следовательно, и уравнений, определяют из соотношения n = p – (q – 1), где по-прежнему p — число ветвей, а q – число узлов. Таким образом, МКТ позволяет понизить порядок системы уравнений на (q – 1). После решения системы уравнений относительно контурных токов определяют токи в ветвях, предварительно задав их условные положительные направления.

Например, для схемы (рис. 1.3), имеющей три независимых контура I, II и III с контурными токами I₁₁ , I₂₂ и I₃₃ в них, система уравнений имеет вид

R₁₁ I₁₁ + R₁₂ I₂₂ + R₁₃ I₃₃ = E₁₁ ,

R₂₁ I₁₁ + R₂₂ I₂₂ + R₂₃ I₃₃ = E₂₂ , (1.6)

R₃₁ I₁₁ + R₃₂ I₂₂ + R₃₃ I₃₃ = E₃₃ ,

где

E₁₁ = E₁ – E₂ , E₂₂ = E₂ , E₃₃ = –E₅ ;

R₁₁ = R₁ + R₂ , R₂₂ = R₂ + R₃ + R₄ , R₃₃ = R₄ + R₅ ;

R₁₂ = R₂₁ = –R₂ , R₂₃ = R₃₂ = –R₄ , R₁₃ = R₃₁ = 0

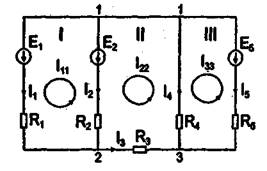Рис. 1.3

Токи в ветвях при указанных на схеме условных положительных направлениях:

I₁ = I₁₁ , I₂ = I₂₂ – I₁₁ , I₃ = I₂₂ ,

I₄ = I₂₂ – I₃₃ , I₅ = –I₃₃

Если некоторые токи в ветвях окажутся отрицательными, его означает, что действительные направления токов в них противоположны условно принятым.

1.3.2 Метод узловых потенциалов (МУП)

Ток в любой ветви электрической цепи можно определить по известным потенциалам узлов, к которым она подключена, или напряжению между этими узлами.

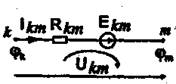
Согласно второму закону Кирхгофа для любой ветви электрической цепи, схема которой приведена на рисунке, при заданных условных положительных направлениях ЭДС, тока и напряжения и указанном направлении обхода контура можно написать уравнение -U_km + R_km I_km = E_km , откуда

I_km = (E_km + U_km )/R_km = [E_km + (φ_k – φ_m )]G_km (1.8)

где U_km = (φ_k - φ_m ) — напряжение между узлами «k» и «m», а φ_k и φ_m — потенциалы этих узлов, причем φ_k > φ_m G_km = 1/R_km – проводимость ветви.

Метод расчета электрических цепей, в котором в качестве неизвестных принимают потенциалы узлов схемы, называют методом узловых потенциалов. Метод более эффективен по сравнению с методом контурных токов в случае, если число узлов в схеме меньше или равно числу независимых контуров, так как в любой электрической цепи потенциал одного из узлов можно принять равным нулю, а число узлов, потенциалы которых следует определить относительно этого узла, станет равным (q -1).