Реферат: Электрические цепи постоянного тока

G₁₁ φ₁ + G₁₂ φ₂ + G₁₃ φ₃ + … + G_{1 n} φ_n = I_{y 1} ,

G₂₁ φ₁ + G₂₂ φ₂ + G₂₃ φ₃ + … + G_{2 n} φ_n = I_{y 2} , (1.9)

G_{n 1} φ₁ + G_{n 2} φ₂ + G_{n 3} φ₃ + … + G_nn φ_n = I_yn

где n = (q - 1); φ₁ , ф₂ …φ_n — потенциалы 1, 2, … n узлов относительно узла q, потенциал которого принят равным нулю; G_kk — сумма проводимостей всех ветвей, подключенных к узлу k; G_kj = G_jk — сумма проводимостей ветвей между узлами «j» и «k», взятая со знаком «минус». Если же между узлами «j» и «k» нет ветвей, то принимают G_kj = G_jk = 0; I_yk — узловой ток, равный сумме токов всех ветвей, содержащих источники ЭДС и подключенных к узлу «k», причем каждый из них определяется по уравнению (1.8) при U_km = 0. Токи, направленные к узлу, берут со знаком «плюс», а от узла — со знаком «минус».

После решения системы (1.9) относительно узловых потенциалов определяют напряжения между узлами U_km и токи в ветвях в соответствии с (1.8). Токи в ветвях, не содержащих источников ЭДС, определяют аналогично, полагая в уравнении (1.8) E_km = 0.

Например, для электрической цепи (см. рис. 1.3), если принять потенциал узла 3 равным нулю (φ₃ = 0), система уравнений будет иметь вид

G₁₁ φ₁ + G₁₂ φ₂ = I_{y 1} , (1.10)

G₂₁ φ₁ + G₂₂ φ₂ = I_{y 2} ,

где

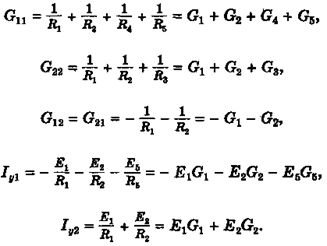
Метод узловых потенциалов особенно эффективен при расчете электрических цепей с двумя узлами и большим количеством параллельных ветвей, при этом, если принять потенциал одного из узлов равным нулю, например, j₂ = 0, то напряжение между узлами будет равно потенциалу другого узла

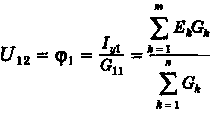
(1.11)

где п — число параллельных ветвей цепи, а m — число ветвей, содержащих источники ЭДС.

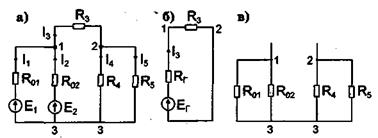
Рис. 1.4

1.3.3 Метод эквивалентного генератора (МЭГ)

Метод позволяет в ряде случаев относительно просто определить ток в какой-либо одной ветви сложной электрической цепи и исследовать поведение этой ветви при изменении ее сопротивления. Сущность метода заключается в том, что по отношению к исследуемой ветви сложная цепь заменяется эквивалентным источником (эквивалентным генератором — ЭГ) с ЭДС Е_г и внутренним сопротивлением R_г .

Например, по отношению к ветви с резистором R₃ электрическую схему, приведенную на рис. 1.4, а, можно заменить эквивалентной (см. рис. 1.4, б).

Если известны ЭДС и сопротивление эквивалентного генератора, то ток ветви может быть найден как

I₃ = E_г / (R_г + R₃ ) (1.12)

и задача сводится к определению значений Е_г и R_г .

Уравнение (1.12) справедливо при любых значениях сопротивления резистора R₃ . Так, при холостом ходе ЭГ, когда узлы 1 и 2 разомкнуты, I₃ = 0 и Е_г = U₀ , где U₀ = (φ₁ – φ₂ ) — напряжение холостого хода эквивалентного генератора, φ₁ и φ₂ — потенциалы узлов 1 и 2 в этом режиме.

При коротком замыкании ветви (R₃ = 0) ток в ней I_кз = E_г /R_г = U₀ /R_г ,откуда внутреннее сопротивление ЭГ R_г = U₀ /I_кз . Таким образом, для определения параметров эквивалентного генератора необходимо рассчитать любым из известных методов потенциалы узлов φ1 и φ2 в режиме холостого хода ЭГ и ток короткого замыкания в исследуемой ветви.

Приведенный метод определения параметров эквивалентного генератора является наиболее универсальным, однако в ряде случаев сопротивление R_г , проще рассчитать как эквивалентное сопротивление между разомкнутыми узлами исследуемой ветви сложной цепи в предположении, что все источники ЭДС в цепи закорочены, как показано на рис. 1.4, в.

Литература

1. Иванов И. И., Лукин А. Ф., Соловьев Г. И.

И 20 Электротехника. Основные положения, примеры и задачи. 2-е изд., исправленное. — СПб.: Издательство «Лань», 2002.

2. Иванов И. И., Равдоник В.С.