Очевидно, що активна потужнiсть P = 0 (як середнє значення синусоїдної функцiї на iнтервалi часу T ). Визначимо енергiю магнiтного поля в iндуктивностi:

.

(Замiна змiнних у межах: при , ; при , ).

Отже

.

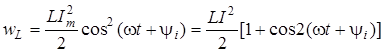Залежностi миттєвих значень u , i , p , в iндуктивностi за часом зображено на рис.8. Проаналiзуємо цi часовi дiаграми: протягом першої чвертi перiоду (вiдлiк вiд точки t* ), коли струм у колi збiльшується, має мiсце заряд iндуктивностi, тобто накопичення енергiї в магнiтному полi за рахунок джерела. Миттєва потужнiсть при цьому додатна i досягає максимального значення .

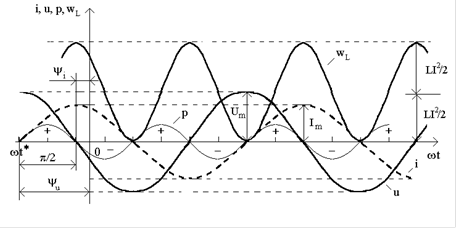
Рисунок 8

У момент часу () енергiя, накопичена в магнiтному полi, також досягає максимального значення . Пiсля цього впродовж другої чвертi перiоду вiдбувається зменшення струму та миттєвої енергiї, тобто розряд iндуктивностi; миттєва потужнiсть у цi моменти вiд'ємна. Оскiльки енергiя в системi не витрачається (P = 0), то зменшення означає, що енергiя повертається до джерела. Далi процес повторюється. Таким чином, вiдбувається коливання енергiї мiж джерелом та iндуктивнiстю, причому активна потужнiсть, яка надходить до iндуктивностi, дорівнює нулю.

Подамо миттєвi значення струму та напруги через комплекснi амплiтуди:

; .

.

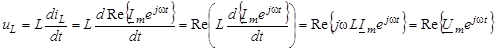З останнього виразу можна зробити такi висновки:

1) операцiя диференцiювання дiйсної функцiї часу за t еквiвалентна множенню на величину комплексно-часової функцiї;

2) оскiльки рiвнi мiж собою реальнi частини, рiвнi також i вектори: . Тодi маємо закон Ома в комплекснiй формi:

, (4)

де - комплексний опiр iндуктивностi.

Розглянемо фазовi спiввiдношення комплексних амплiтуд струму та напруги в iндуктивностi. Для цього запишемо у показниковiй формi:

.

Цей вираз пiдтверджує висновок щодо фазового зсуву мiж комплексними амплiтудами та на кут (рис.9а). Нагадаємо, що фазовi кути вiдраховують вiд осi +1 проти ходу годинникової стрiлки.

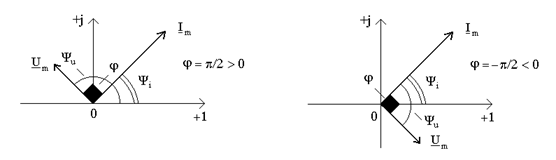
а) б)

Рисунок 9

Знайдемо вираз для комплексної амплiтуди струму, користуючись спiввiдношенням: .

.

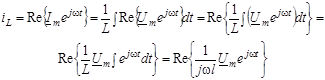Скоротивши вираз на множник , отримуємо ще один запис закону Ома в комплекснiй формi:

,

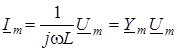де - комплексна провiднiсть iндуктивностi.

Зазначимо, що операцiя iнтегрування дiйсної функцiї часу при переходi до комплексно-часової функцiї замiнюється операцiєю дiлення на величину .

6. Синусоїдний струм в ємності

Нехай через ємнiсть протiкає струм . Миттєвi значення струму та напруги в ємностi пов'язанi спiввiдношеннями: