Реферат: Электростатическое взаимодействие точечных зарядов
А = q2 /32π2 ε0R04, (19)
будет учтена в конце работы.
Подстановки (16) с образованием относительных распределений типа (18) применим также к W1 и W2 (формулы (12)); получим, соответственно, w1 и w2 :
w1 = r1 –4 = 1/(x2 + y2 )2 ; w2 = r2 –4 = 1/[(1 – x)2 + y2 ]2 . (20)
Найдёмсоотношение
w = (w1 + w2 + w3 )/(w1 + w2 ) = 1+ w3 /(w1 + w2 ) = 1 + r1 r2 (r1 2 + r2 2 – 1)/(r1 4 + r2 4 ), (21)
которое представляет собой некоторую поверхность. Участок этой поверхности внутри и вблизи центральной зоны взаимодействия показан на рис. 2 в пределах изменения x от –1 до 1, и y от –2 до 2.
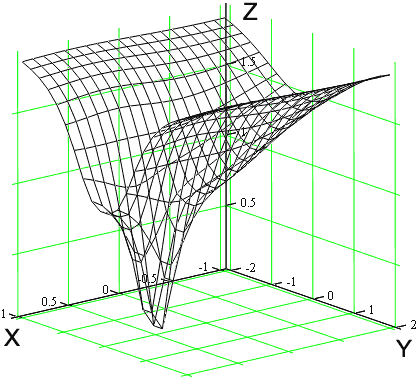
Рис. 2. Отношение w объёмной плотности энергии в системе двух одноимённых взаимодействующих зарядов к сумме энергий невзаимодействующих зарядов
Заряды расположены в точках с координатами (0, 0) и (1, 0). Если бы энергия w3 отсутствовала, то рассматриваемое отношение имело вид плоскости w = 1 (см. формулу (21)).
Как видно из рис. 2 и формулы (21), значение w равно нулю в центре отрезка R0 (x = 0,5; y = 0); w = 1 на окружности, вписанной между зарядами; w = 2, максимально достижимое значение при x, y → ∞. Взаимодействие зарядов существенно дополняет сумму их собственных энергий и положительными, и отрицательными вкладами; при отталкивании зарядов энергия поля как бы «уходит» из центральной зоны наружу. Однако,
|w3 /(w1 +w2 )| ≤ 1, (22)
то есть плотность энергии взаимодействия зарядов в каждой точке поля никогда не превышает суммы плотностей их собственных силовых полей. Новая деформированная структура поля обладает большей энергией, чем недеформированная. Поле «стремится» избавиться от избыточной энергии, и отсюда возникают силы взаимодействия. Механизм образования деформированной «надструктуры» w3 целиком определяется принципом суперпозиции (векторным сложением напряжённостей полей).
Выясним, как соотносятся полные энергии взаимодействия внутри центральной зоны и за её пределами? Ответ на него может дать интегрирование по формуле (17) с учётом (16) и (18). Интеграл по y после подстановки
dV = 2πR0 3 ydydx, y2 = z, 2ydy = dz (23)
в формулу (17) становится табличным. Вводя обозначения,
a = 1, b = x2 + (1 – x)2 , c = x2 (1 – x)2 , (24)
имеем
A ∫V w3 dV = A∙2πR0 3 ∫x dx ∫z (± c1/2 + z) dz / (az2 + bz + c)3/2 = B ∫x I(x)dx, (25)
I(x) = (± c1/2 – z)/(4ac – b2 )(az2 + bz + c)1/2 |0 ∞ = [1/(1 – 2x)2 ] ± [1/(1 – 2x)2 ], (26)
B = (q2 ∙4πR0 3 /32π2 ε0 R0 4 ) = q2 /8πε0 R0 . (27)
Смысл I(x) – потенциальная энергия на единицу длины вдоль x, просуммированная по бесконечной плоскости (с координатой x), перпендикулярной оси x. С другой стороны, это – осреднённая в названной плоскости относительная сила воздействия на заряд слоем поля, толщиной dx. График I(x) показан на рис. 3.
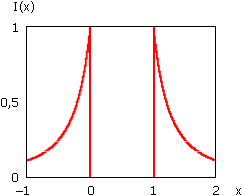
Рис. 3. Изображение I(x) по формуле (26)
Интеграл (25) вычисляется в пределах от нуля до бесконечности. При этом надо различать три области по x:
1) область отрицательных значений (–∞ < x < 0, знак плюс перед c1/2 );
2) область между зарядами (0 ≤ x ≤ 1, знак минус перед с1/2 );
3) область оставшихся положительных значений (1 < x < ∞, знак плюс перед c1/2 ).
Аналогично применяются знаки в правой части (26).