Реферат: Электростатическое взаимодействие точечных зарядов
I1, 3 (x) = q2 /4πε0 R0 (1 – 2x)2 . (28)
Во второй области
I2 (x) = 0. (29)
Из формул (3), (17), (25) следует, что и в других случаях, каковы бы ни были величины и знаки зарядов, потенциальная энергия в области 2 равна нулю, причём компенсация положительных и отрицательных вкладов происходит в каждой плоскости x = const. Этот факт заслуживает особого внимания, так как в области 2 происходят существенные деформации поля. Таким образом, оказывается, что вся энергия взаимодействия сосредоточена в областях 1 и 3 поровну. Воздействие на заряды осуществляется не из пространства между зарядами, а из пространства снаружи.
Интегрирование выражения (25) по x в пределах от –∞ до +∞ приводит к результату
∫I1,3 (x)dx = (q2 /4πε0 R0 )·(0,5+0,5) = q2 /4πε0 R0 = U. (30)
Независимое интегрирование (17) воспроизводит (ещё раз!) закон Кулона для U и подтверждает предположение (15). Интересная деталь: в выражении (17) значимые для взаимодействия зарядов величины (q и R0 ) выводятся за знак интеграла, образуя необходимую энергию U, а сам интеграл, в конечном счете, оказывается равным единице при любых обстоятельствах. Формулы (25)...(30) демонстрируют вероятностный характер распределения энергии внутри поля, и объясняют причину совпадения расчётов энергии взаимодействия двумя разными способами, упомянутыми во введении. Так и должно быть, потому что напряжённости E обладают свойствами квантовомеханических амплитуд [14].
При рассмотрении взаимодействия разноимённых зарядов значение W3 (см. формулу (13)) становится положительным внутри центральной зоны, и отрицательным за её пределами. Знак минус приобретает потенциальная энергия U.
Функция W3 применяется также в вариационной процедуре (принципе наименьшего действия) для электрической составляющей электромагнитного поля (см. [5, 12]). В этом случае W3 с самого начала рассматривается, как распределение вероятностей взаимодействия по точкам пересечения напряжённостей E1 и E2 в пространстве. Результат такой процедуры для статического поля тот же, как по форме (вычисление функции Лагранжа по формулам (25)...(30)), так и по содержанию (закон Кулона).
Р.Фейнман в своей Нобелевской лекции [13] отмечает: «...электродинамику можно построить... различными способами, – на основе дифференциальных уравнений Максвелла, (или) на основе различных принципов наименьшего действия с полями, и без полей... Самые фундаментальные законы физики после того, как они уже открыты, все-таки допускают такое невероятное многообразие формулировок, по первому впечатлению не эквивалентных, и всё же таких, что после определенных математических манипуляций между ними всегда удаётся найти взаимосвязь. Чем это можно объяснить, – остаётся загадкой. Думается, что здесь каким-то образом отражается простота природы. Может быть, вещь проста только тогда, когда её можно исчерпывающим образом охарактеризовать несколькими различными способами, ещё не зная, что на самом деле ты говоришь об одном и том же».
Вернёмся к формуле (4а) и попытаемся на её основе выстроить гипотезу для понимания механизма размещения внутри поля энергии взаимодействия U. Будем считать, что плотность ρ описывает, как заряды, изначально создающие поле, так и заряды, образованные (наведенные) полем в физическом вакууме. Теперь подынтегральное выражение (4а) можно положить равным нулю в каждой точке поля,
(ε0 E2 – φρ)/2 = 0; (31)
при этом дислокация ρ не будет точечной, но закономерности Е и φ, определённые формулами (2) и подтверждённые экспериментально, не подлежат пересмотру. Совпадение «точечных» расчётов с опытом имеет место и для неточечных, но сферически симметричных источников. Кроме того, мы полагаем, что суммарный наведенный заряд, состоящий из равного количества положительных и отрицательных зарядов, равен нулю.
Из выражения (31) по известным значениям E и φ можно найти некоторые свойства одной из моделей физического вакуума – «поляризованного» вакуума [8]. Согласно этой модели возбуждение вакуума заключается «в узком смысле слова, в рождении виртуальных пар заряженных частиц-античастиц (напр., пар электрон – позитрон) из вакуума... Этот эффект аналогичен поляризации диэлектрической среды внесённым в неё зарядом...». Из работы [3] следует, что в данной среде можно ожидать появления связанных зарядов с объёмной плотностью ρ'. При отсутствии сторонних зарядов в рассматриваемой части диэлектрика,
ρ' = –ε0 ·(Egradχ)/(1 + χ). (32)
Здесь χ – диэлектрическая восприимчивость (неоднородной, но изотропной) среды.
Преобразуем второй член в формуле (31), используя (2) и (9),
φρ = (φ1 + φ2 )(ρ1 + ρ 2 ) = φ1 ρ1 + φ2 ρ2 + φ1 ρ2 + φ2 ρ1 = φ1 ρ1 + φ2 ρ2 + φρ12 ', (33)
ρ12 ' = (φ1 ρ2 + φ2 ρ1 )/φ. (34)
Расписывая первый член формулы (31), имеем сумму W1 , W2 , W3 (см. формулы (3),(12),(13)). Таким образом, можно написать три равенства,
φ1 ρ1 = 2W1 , φ2 ρ2 = 2W2 , φρ12 ' = 2W3 . (35)
Два первых равенства в (35) можно дополнить соотношениями
∫V ρ1 dV = Q1 , ∫V ρ2 dV = Q2 ; (36)
в данной работе они не рассматриваются. Представляет, однако, интерес по теме статьи крайнее справа равенство в (35). Значение плотности
ρ12 ' = 2W3 /φ (37)
можно трактовать, как источник поля с энергетической плотностью W3 , образованный внешними силами. Вследствие того, что силовое поле от ρ12 ' не выходит из замкнутой поверхности (8), суммарный по объёму заряд от этой плотности должен равняться нулю. Ниже на рис. 4а (S) и рис. 4 б (Q) представлены расчётные значения ρ12 '.
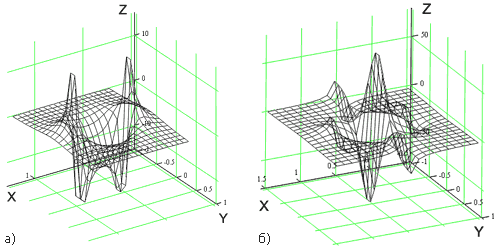
Рис. 4. Объёмная плотность ρ12 ': а) вычисленная для одноимённых зарядов по формуле (37) в пределах (–0,5 < x < 1,5; –1 < y < 1); б) вычисленная для разноимённых зарядов
Заряды расположены в плоскости (x, y) в точках с координатами (0, 0) и (1, 0). Для перехода к абсолютным величинам значения плотности на графике следует умножить на константу (q/4πR0 3 ). Здесь имеется неопределённость в плоскости, перпендикулярной оси x, посередине между зарядами, где φ1 + φ2 = 0.