Реферат: Элементы теории устойчивости

По этой причине при исследовании устойчивости в таких цепях нелинейное сопротивление сS – образной ВАХ представляют в виде последовательного соединения его дифференциального сопротивления и малой начальной индуктивности.

У элементов с N – образной ВАХ напряжение является неоднозначной функцией тока. Здесь при определенных токах при их плавных изменениях теоретически возможны скачкообразные изменения напряжения, которые, однако, в реальных системах предовращаются наличием малой паразитной емкости. Поэтому при исследовании устойчивости в таких цепях нелинейное сопротивление с ВАХ N – типа заменяют эквивалентной схемой с параллельным соединением дифференциального сопротивления и малой паразитной емкости.

Устойчивость точки равновесия электрической дуги.

? ???????? ??????? ???? ??????????? ???? ?????????? ????????????? ???? ? ??? S - ????. ? ?????? ?????????? ????????????? L ???? ????? ????????????? ?????, ?????????????? ?? ???. ??????. ????????? ???? ?? ????????? ?????? ???????? ????? ???:
? ????????? ?????????? ??? ? ???? i ?? ?????? ?????????? ?? ??????? t :
??????? ????????? ?????? ???:
??????? ????????? ???????????? ????????, ??????? ??? ????
??? ξ( t) ? ????? ??????????; ????? ???????:
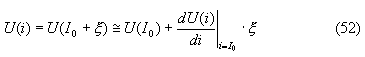???????? ??????? U(i) ? ??? ? ????? I ­­_{0 ­} ?? ???????? ????? ?????????? ξ ? ??????????? ?????????? ??????? ??????? ???????, ??????????? ????? ??????? ????? ??????? ???????? ???????:

Обозначим величину дифференциального сопротивления нелинейного сопротивления R_d в точке i=I₀ :

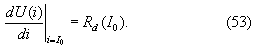????? ?????????? (53), (52), (49) ? (51) ??????? ??????????????? ????????? ????:
???
??????????? ??????? (54) ? ????
??????? ?????????????????? ????????? ???????
? ????? ??????????? ξ (t) ? ????????? ?????:
?????????????, ????????? ???????? ??????? (54) ?????????????? ?????????, ? ???????? ?????????? ??????? (51) ????????? ? ??????? ??????. ???? ??????????? ???????
????????? ??????????? (55) ???????????? ????????:

Последнее выражение представляет собой известный критерий Кауфмана для устойчивой рабочей точки электрической дуги.

Устойчивость решений уравнения Дуффинга.

Запишем уравнение движения неконсервативного нелинейного осциллятора, находящегося под гармоническим внешним воздействием, для случая среды с вязким трением (7.2), (11.1)

1) Формулы с двойными номерами здесь – (7.2), (11.1) - и ниже – (7.5), (3.20), (9.5), (11.3), (11.5) – цитируются по книге [4].

2) ????????? ?????? λ ??????????? ????? ? ????????? ??????? ??? ??????????? ?????? ?????????????????? ?????????.

где символом δ обозначена в соответствии с (7.5) удельная вязкость среды; ω₀ , μ – (3.20), F – (9.5).

?????? ????? ????????? ????? ??????????? ? ???? ????? ???????? ? ?????????? ??????????:

где F₁ , F₂ определяются выражениями (11.3) и справедливы формулы (11.5).

??? ???????????? ???????????? ??? ???????? ????????? ??????????????? ??????? ??? ????????? ????? ?????????? ?????????? ???????????? ?????? ??????????? ??? ??? ????:

где a(t) , b(t) – медленно изменяющиеся функции. Вычислим первую и вторую производные функции y(t) по времени t :

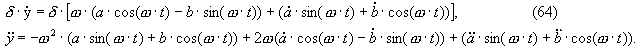
????????? ??????????? ????????? ??????? a(t) , b(t) ? ??????? ????????? δ , ??????????? ? ???????? (64) ?????????? ?????? ???????? ???????:

Подставив последние выражения и (63) в уравнение (61), получим:

Тригонометрический двучлен третьей степени в левой части равенства без учета всех компонент, кроме колебаний с основной частотой ω может быть представлен в следующем виде:

????????? ??? ????????? ? ?????????? ? ???????????? ????????? ? ??????????? ??????????????????? ????????? ??????? ??? ???????????:
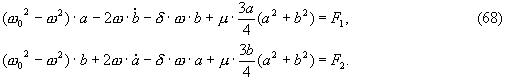??????, ???????? ????????? ???????????? a , b , ????? ???????? ??????? ????????????? ?????????:
?????????? ???????????? ???????:
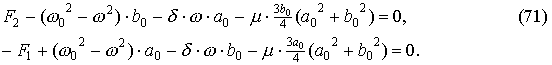????? ??? ??????????? ???????? ???????????? ????????? a_{0 ­­} , b₀ ?? ????????? ??????? (69) ???????? ?????????????? ?????????:
????? ??????? (11.6) ???? ???????? ? ??????? ?????? ??????? ?????? ?????? ????????? ?????????:
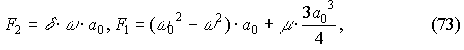??? ???? ?? (71) ???????? ?????????:

совпадающие, как и следовало ожидать, с (11.9). Тогда. Использую (11.5), (73) можно записать формулу (11.10):

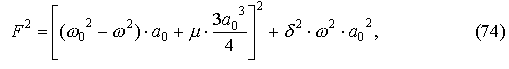
Определяющую резонансную зависимость рассматриваемого осциллятора | a₀ | ( ω ) или его «управляющую» характеристику | a₀ | (F) .

??? ???????????? ???????????? ?????????? ???????????? ????????? ? ??????????? a₀ , b₀ (70), (71) ?????? ?????? ? ???????????? ?? ????? ?????????? ξ (t) ,η (t) :
???
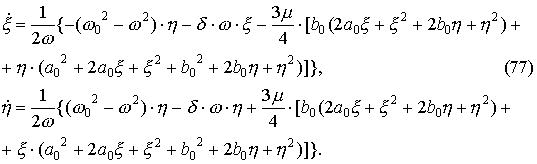????? ?????????? (75) ? ??????????? ????????? (69) ? ????????? ??????? ??? ???????????? ???????? (71), ??????? ?????????? ??????? ???????????? ???????? ? ????????? ????:
??????????? ????????? (77), ????????? ??????? ?????????? (76):
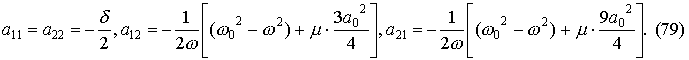??? ?????????? ???????????? a_νm ??? ???????? ??????, ?????????????? ????? (72), ???????????? ???:
????????? ?????????? ? ???????????????? ????? (13), ??????? ??????? ?????????????? ????????? (14), ??????????? ???? ???????????? ???? ??????? (15), (16), ???????????? ???????? ?????????????????? ????????? ? ????:
???
?????????????, ??????????? ? ??????????? ??????? ???????????? ??????????????? ??????? ????? ???????? ???:

или, используя обозначения (79)

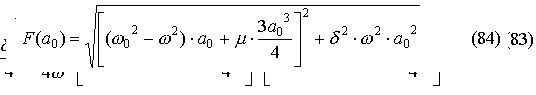?????? ?? ???? ??????? ? ?????? ??????????????? ??????, ????????, ??????????? ??????. ?????? ??????? ??????? ????? ?????????? ???????. ????? ??? ???????????, ????????? ??????????? F(a₀ ) ?? ????????? ??????????? (74):

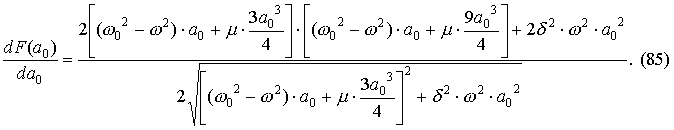
и вычислим производную dF/da₀ :

Последнее выражение легко преобразовать к виду:

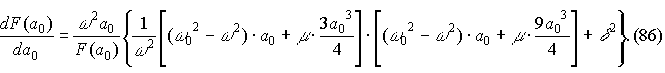
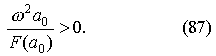???? ?????? ? ???? ??????????? ????????? ??????????? ????????? a₀ (11.6) ???????? ?? ?????? ???? ???????? |a₀ | , ??? ??? ?????? ???????? ??? ?????????? ??????????? ????????????? | a₀ | ( ω ) ???????????? ? ?? ??????????? ????????????? | a₀ | (F) , ?? ??????? ????????? ? ??????????? (86) ?? ??????????. ? ?????????, ???? ??????????? ?? ?????????. ????? ???????, ??????????? ??? ???????? ?????? ? (86) ???????? ????????? ??????????? ?????????????.
?????, ????????? ?????????, ??????????? ? ???????? ?????? ? (86) ? ???????? (83) ?????, ??? ??????? ???????????? ????????? ??????? ??????????????? ???????????.
??? ??????? ??????????????? ???????? ????????

Следовательно, все точки управляющей характеристики осциллятора с положительным наклоном касательной соответствует устойчивым режимам колебаний. На рисунках?????????????? и 12.3 эти ветви изображены сплошными кривыми. «Падающей» ветви характеристики соответствуют неустойчивые колебания. На рис?????????? Эта ветвь представлена пунктиром, а на рис. 12.3 вообще отсутствует.

? ?????????? ?????? ???????? ??????

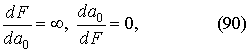имеет место упомянутый ранее «критический» случай, поскольку можно показать, что появляются корни характеристического уравнения с равными нулю вещественными частями. Анализа устойчивости на основе линейного приближения здесь оказывается недостаточно. Устойчивость или неустойчивость в этих точках определяют слагаемые высших порядков малости в уравнениях возмущенного движения.