Реферат: Энергия активации
4) Действие катализатора зависит от его физического состояния и от присутствия посторонних веществ. Промоторы усиливают действие катализатора, а каталитические яды снижают активность катализатора.
5) Смесь катализаторов часто действует значительно сильнее, чем отдельные катализаторы.
1.5 Сущность каталитического действия
Если энергия активации высока, то лишь небольшая доля сталкивающихся молекул имеет энергию, достаточную для того, чтобы произошла реакция, а если она низка, то реагирует большая часть молекул, и поэтому константа скорости будет большой. Из этого следует, что если каким-либо образом можно снизить энергию активации, то реакция должна протекать с более высокой скоростью.
Катализатор - это вещество, которое заставляет реакцию протекать быстрее, снижая энергию активации лимитирующей стадии. Некоторая мера эффективности катализаторов может быть получена при рассмотрении изменений энергии активации различных реакций, которые обусловлены наличием катализаторов. При разложении перекиси водорода в отсутствие катализатора энергия активации равна 76 кДж/моль, и при комнатной температуре разложение протекает очень медленно. Если добавить небольшое количество иодида, происходит та же самая реакция, но с энергией активации 57 кДж/моль, и, таким образом, при комнатной температуре (когда RT = 2,5 кДж/моль) константа скорости лимитирующей стадии увеличивается в
К(катализатор)/К(без катализатора) = е7,6 ≈ 2000 раз.
Более существенное изменение энергии активации происходит при добавлении ферментов к биохимическим системам.
Фермент является биологической молекулой, которая обладает большой эффективностью. Это иллюстрируется изменением энергии активации в реакции гидролиза сахарозы от 107 кДж/моль в присутствии иона гидрооксония до 36 кДж/моль при добавлении небольшого количества фермента сахаразы. Такое изменение энергии активации соответствует изменению значения скорости на 22 порядка.
1.6 Методы расчета энергии активации и предэкспоненциального множителя
В большинстве случаев для расчета энергии активации Еа по экспериментальным данным используют интегральную форму уравнения Вант-Гоффа-Аррениуса (6) или его запись в виде:
lgK = lgKo - Е а/2,303 RT (9)
Следовательно, lgK линейно зависит от обратной абсолютной температуры (см. рисунок)
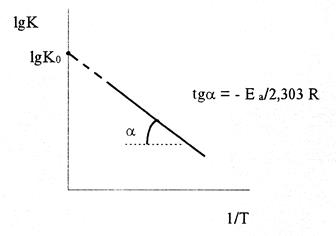
Значение Еа находят по тангенсу угла наклона прямой, проходящей через экспериментальные точки: Е а = -2,303Rtgα.
Предэкспоненциальный множитель К0 определяется отрезком, отсекаемым продолжением прямой на оси ординат при 1/Т = 0.
Если имеются значения константы скорости химической реакции при двух температурах, то из уравнения (9) можно получить:
Еа =(2,303RT1 T2 lgK2 /K1 )/(T2 -T1 ) (10)
Энергия активации Еа имеет размерность энергия/моль и измеряется в единицах Дж/моль. Размерность К0 совпадает с размерностью константы скорости. Теория и экспериментальные данные (для широкого температурного интервала) показывают, что Еа и К зависят от температуры. Однако эту зависимость можно не учитывать, если реакции исследуются в достаточно узком температурном интервале.
Изложенный выше метод расчета Еа предполагает, что константы скорости реакций при различных температурах известны.
Однако, есть способ расчета Еа , так называемый метод трансформации, который не требует знания K=f(T).
Пусть при температурах T1 и T2 в смесях одного и того же начального состава протекает химическая реакция. Если к моментам времени τ1 и τ2 реакция прошла на одну и ту же глубину, то есть изменения концентраций исходных веществ или продуктов реакции одинаковы, то отношение скоростей реакции равно:
W1 / W2 = (dC/dτ1 ) /(dC/dτ2 ) = dτ2 / dτ1 .(11)
Заменим в уравнении (11) скорости реакций при заданных температурах соотношением (4)
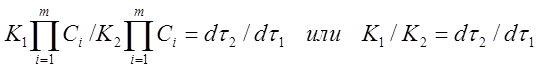 .(11а)
.(11а)
Таким образом, отношение K1 /K2 можно заменить отношением τ1 / τ2
Подставим в отношение (11а) значения констант скорости при температурах T1 и Т2 , используя уравнение Аррениуса (5):
K0 exp(-Ea /RT1 )/ K0 exp(-Ea/RT2 ) = d τ2 / d τ1 .
Полагая, что для узкого температурного интервала К0 и Еа = const находим
ехр[-Ea/R(l/T1 - 1/Т2)] = dτ2 / dτ1 .(12)