Реферат: Физика 9-10 класс
Лекция 22
20. Стоячие волны. Рефракция
21. “Внутреннее движение” квантового состояния
22. Квантование момента импульса
23. Классический гироскоп в магнитном поле
Лекция 2
Лекция 2
3.1. Возникновение волны. Группа волн
???????, ?????? ?????????? ???????? ????? ?? ??????????? ????. ?? ????? ?????? ??????? ????????????? ????????. ??? ????? ???????? ????????? ????? ?????? ????? ????? ??????? ??????, ??????, ? ???? ?? ????????? ???????????? ????. ?? ????? ??????? ????? ?????? ???????????????? ?????, ??????? ????? ??????? ?????????. ?? ????????? ? ??????????? ?? ?????????? ?? ????? ??????? ????? ?????????? ??? ??, ??? ? ? ????? ??????????????.
Однако, это не совсем такая волна, о которой мы говорили. Синусоидальная волна не должна иметь начала или конца, чего, конечно, нельзя сказать о волне, возникшей при падении камня в воду.
x
0 r
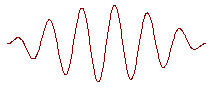
Совсем не обязательно, чтобы такая группа волн имела показанную на рисунке динамику увеличения и уменьшения амплитуды, показанный профиль. Для нас важнее понять, почему волна в этом случае имеет название “группы”. Для этого надо вспомнить возникновение биений, которые наблюдаются при сложении колебаний близких частот. Разность фаз таких колебаний
изменяется достаточно медленно. Между моментами, когда амплитуда суммарных колебаний
со средней частотой 
обращается в нуль, проходит достаточно много (по сравнению с периодом колебаний) времени:
; 
;
,
поскольку разность частот колебаний много меньше средней частоты: 
. Поэтому мы наблюдаем приблизительно гармонические колебания с медленно изменяющейся амплитудой. Амплитудой в этом случае называется произведение подчеркнутых сомножителей в выписанных выше выражениях.
Предположим теперь, что вдоль некоторого направления распространяются плоские волны с близкими длинами волн. Соответственно и частоты распространяющихся с ними колебаний будут близкими. В каждой точке, например, в точке x = 0 будут наблюдаться биения:
