Реферат: Физика и музыка

РЕФЕРАТ

По Физике

По теме : Физика и Музыка

Студентки группы 1м4

Колледжа Государственной

Службы №337

План:

1.

2.

3.

МУЗЫКАЛЬНЫЕ ЗВУКИ

Постановка вопроса. В чем различие между музыкой и шумом? Установить различие между музыкой и шумом довольно трудно, так как то, что может казаться музыкой для одного, может быть просто шумом для другого. Не­которые считают оперу совер­шенно немузыкальной, а дру­гие любят ее. Ржание лошади или скрип нагруженного лесом вагона может быть шумом для большинства людей, но музыкой для лесопромышленника. Любя­щим родителям крик новорож­денного ребенка может казать­ся музыкой. Но для большин­ства из нас такие звуки пред­ставляют просто шум. Однако большинство людей согласится с тем, что звуки, возбуждаемые колеблющимися струнами, язычками, камерто­нами, столбами воздуха и вибрирующими голосовыми связками певца, музыкальны. Но если так, то что же существенно в воз­буждении музыкального звука, или тона?

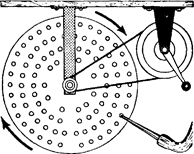
Для того чтобы ответить на этот вопрос, воспользуемся сире­ной, изображенной на рис.1. Будем быстро вращать диск с по­стоянной скоростью и вдувать струю воздуха через стеклянную трубку в ряды отверстий диска по порядку. Мы увидим, что ряды, имеющие отверстия, расположенные на равном расстоянии друг от Друга, производят приятные музыкальные звуки, а звук от ряда неравномерно расположенных отверстий представляет шум.

Когда поток воздуха проходит сквозь отверстие, то на противоположной стороне диска получается сгущение. Воздух не может пройти через промежутки между отверстиями, и в эти моменты возникают разрежения. Такие воздушные толчки производятся через одинаковые промежутки времени рядами равномерно распо­ложенных отверстий, другие же ряды дают толчки через различ­ные времена.

Таким образом, наш опыт показывает, что для возбуждения музыкального звука существенно, чтобы колебания происходили через равные промежутки времени. Колебания струн, камертонов и т. н. имеют такой характер; колебания поездов, вагонов с лесом и т. п. происходят через неправильные, неравномерные промежут­ки времени, и производимые ими звуки представляют только шум.

(рис. 1 сирена)

Что называется высотой тона? Высота тона характеризует, нисколько «тонок» или «груб» звук. Для того чтобы получить самые высокие тоны рояля, мы ударяем по клавишам, расположен­ным на конце правой части клавиатуры; самые низкие тоны полу­чаются с левого края. Чем объясняется это различие в высоте тона?

Для того чтобы помочь ответить на этот вопрос, воспользуемся опять той же сиреной. Диски имеют ряды в 24, 30, 36 и 48 отвер­стий, расположенных на одинаковых расстояниях. Вращая диск с постоянной скоростью, будем вдувать воздух по порядку в каж­дый ряд отверстий, начиная с внутреннего ряда. Каждый ряд воз­будит музыкальный тон, причем каждый следующий ряд даст тон выше предшествующего. Теперь будем изменять скорость враще­ния диска при вдувании воздуха в один и тот же ряд. Мы увидим, что увеличение скорости повышает тон, уменьшение понижает тон. Что показывают результаты этого опыта?

Увеличивая скорость диска или пользуясь рядом с большим количеством отверстий, вы увеличиваете число толчков или волн в секунду, посылаемых через воздух. Таким образом, оказывается, что высота тона звука зависит от числа толчков (импульсов) или волн в секунду, приходящих от звучащего тела к уху. Так как вы­соту тона, как таковую, трудно измерять, физики предпочитают выражать ее через частоту, которую измерить легко.

Можно задать вопрос: распространяются ли звуки различных частот с одинаковыми скоростями? Если высокие звуки распро­страняются быстрее или медленнее, чем низкие звуки, то, как будет звучать находящийся в некотором отдалении оркестр, в состав которого входят бас и флейта? Действительно ли оркестр звучит так? Каково ваше заключение?

Что называется мажорной диатонической гаммой? Возможно, что некоторые из вас узнали в тонах, возбуждаемых нашей сире­ной, топы мажорного аккорда. Первые три тона, производимые ря­дами в 24, 30 и 36 отверстий, составляют мажорное трезвучие. Диск с 8 рядами отверстий, а именно с 24, 27, 30, 32, 36, 40, 45 и 48 от­верстиями воспроизвел бы все тоны мажорной диатонической гам­мы. Даже при вращении с различными постоянными скоростями в каждом случае воспроизводилась бы точно эта гамма. Если бы диск вращался со скоростью 10-у об/сек, то частоты были бы такими, как показано в таблице ниже.

Число отверстий Вк	24	27	30	32	36	40	45	48
Частота колебаний В секунду	256	288	320	341,3	384	426,6	480	512
Отношение чисел ко­лебаний	1	9/8	5/4	4/3	3/2	5/3	15/8	2
Тоны	С	D	Е	F	G	А	В	С `
Названия	до	ре	м и	фа	соль	ля	си	до

тон, имеющий частоту в 256 колебаний в секунду, называется до (С) средней октавы. Гамма, приведенная в этой таблице, известна под названием до мажор, где С является основным тоном, или тоникой.

Числа 24, 27, 30 и т. д. являются относительными числами коле­баний, частоты являются абсолютными числами колебаний. Отно­шения получаются путем деления каждого относительного числа колебаний на первое (24). Эти отношения одинаковы для всех ма­жорных гамм, независимо от того, с какого основного тона они на­чинаются.

Гаммы всегда называются по тонике, например: до мажор, ре мажор и т. д. Полная гамма до мажор и соответствующие названия (применимые к любой гамме) вместо с отношениями колебаний и частотами приведена в таблица. Ближайшим тоном, следующим за С', является D' (ре'), частота которого 576 колебаний в секунду.

Тоны С, Е и G образуют тоническое трезвучие гаммы до мажор, так как нижний тон является тоникой этой гаммы. Отметьте, что 24:30:36=4:5:6. Любая группа тонов с таким отношением частот составляет мажорное трезвучие. Обратившись к гамме до мажор,

(рис. 2 Соотношения между тонами мажорной диагностической гаммы)

мы можем обнаружить в ней еще два других мажорных трезвучия:

F, А и С' — субдоминантное трезвучие, и G, В и D1 — доминант­ное трезвучие. Так как эти три трезвучия содержат все тоны мажор-

пой гаммы, то можносказать, что эта гамма на них основана. С по­мощью рис. 2, на котором сведены все эти данные, можно уяс­нить себе все соотношения.

Что называется музыкальным интервалом? Мы уже знаем, что диск нашей сирены дает мажорную гамму независимо от ско­рости вращения; иначе говоря, существенное значение имеют не абсолютные частоты, а относительные. До тех пор, пока остаются постоянными отношения колебаний, сохраняются и соответствую­щие отношения между высотами тонов.

(Рис. 3. клавиши рояля)

Термин музыкальный интервал относится к относительным ча­стотам двух тонов, а относительная частота представляет собой отношение, а не разность между частотами. Когда это отношение равно 2:1, как в случае С':С==512:256, или 48:24, интервал со­ставляет октаву. Отношение между 3-м и 1-м тонами мажорной гаммы равно 5:4 (30:24), как в случае Е:С. Этот интервал пред­ставляет собой большую терцию. Попробуйте отыскать две другие большие терции в гамме до мажор.

Другими важными интервалами являются: кварта (32:24, или 4/3), квинта (36:24, или 3/2), секста (40:24, или 5/3) и малая терция (36:30, или 6/5), как С:Е в гамме до мажор. Очевидно, октава — это восьмой интервал. Отметьте, сколько сумеете, ука­занных интервалов в гамме до мажор. Музыкант может сразу опо­знать эти интервалы, если взять их на музыкальном инструменте или если спеть их.

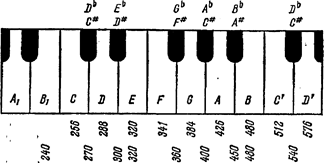
Для чего служат черные клавиши на рояле и в органах? Как мы уже указали, в качестве основного тона мажорной гаммы можно взять любой тон гаммы до мажор. Если взять тон В1 за тонику, то частота будет 240 колебаний в секунду (480:2); второй тон будет со­ставлять 9/8 от 240, или 270 колебаний в секунду; третий — 5/4 от 240, или 300 колебаний в секунду, и т. д. На рис. 3 сопостав­лены гаммы ре мажор и до мажор. Заметьте, что только для трех белых клавиш частоты соответствуют частотам нашей вновь обра­зованной гаммы, а именно: В1 Е и В. Другие же частоты попадают в промежутки между частотами гаммы до мажор, приблизительно в середину.

Таким образом, если мы будем играть гамму ре мажор, то нам необходимо добавить между белыми клавишами еще пять других. Такими клавишами и являются черные, показанные на рисунке. Черная клавиша между C и D обозначается либо С# (до-диез) или DЬ (ре-бемоль); черная клавиша между F и G обозначается как F# или GЬ и т. д. Без применения черных клавиш игра на рояле, пение и сочинение музыкальных произведений ограничивались бы толь­ко одной гаммой — натуральной гаммой до мажор. Она так назы­вается потому, что не содержит ни диезов, ни бемолей.

Что называется равномерно темперированной гаммой? Отме­тим, что на рис. 29.3 показаны как гамма ре мажор, так и гаммы до мажор и си мажор. Приведенные здесь частоты для гаммы ре мажор ставят задачу, которая не разрешается введением черных клавиш. Частоты для Ми и ля в гамме ре мажор не совпадают с частотами их в гамме до мажор. Таким образом, если мы хотим сыграть гамму ре мажор совершенно точно, нам необходимо до­бавить еще клавиши. Если мы будем рассчитывать идеальные гаммы для всех клавиш, в том числе и для черных, взятых за исход­ные, то мы обнаружим еще много других расхождений, и для того, чтобы сыграть все гаммы идеально, следовало бы добавить еще око­ло 70 клавиш на октаву. Разумеется, играть на таком сложном инструменте было бы очень трудно.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--