Реферат: Физика и музыка

что составляет приблизительно 1,06. Таким образом, частоту любого тона гаммы можно получить, умножив частоту предыдуще­го, более низкого тона на 1,06.

Какова стандартная высота тона? Стандарты для высоты тона существуют всего па протяжении менее чем трех поколений, а сделались общепринятыми едва ли 25 лет назад. Как правило, для физиков стандартной высотой тона является С — 256 колебаний в секунду. Большинство из вас знает, что музыкальные инстру­менты настраиваются на определенную частоту для средней октавы. Для физиков ля имеет 420,6 колебания в секунду. 13 музы­кальных кругах пользовались различными стандартами. Кон­цертная высота топа, которой сейчас редко пользуются, состав­ляла 271 колебание в секунду для до средней октавы, что дает для ля около 450, т. е. слишком высокий тон. Международный стан­дарт высоты тона давал для ля 435 колебаний в секунду, однако в настоящее время во всем мире применяется стандартная частота, принятая Американской федерацией музыкантов, дающая для ля 440 колебаний в секунду. Хотя это и ниже концертной высоты тона, однако некоторые сопрано затрудняются спеть арии, сочиненные старыми мастерами, при таком стандарте высоты тона.

Что называется эффектом Доплера? Наблюдали ли вы когда-нибудь внезапное понижение слышимого тона автомобильного

(Рис.4. Применима ли к эффекту Доплера зависимость v = nl )

гудка, гонга пожарной машины, свистка или звонка поезда, когда транспорт быстро проносится мимо вас? Даже шум от машины как будто понижает тон, когда машина быстро проезжает мимо вас по дороге. Как объяснить все эти явления? Очевидно, изменение высоты тона вызвано относительным движением источника звука и наблюдателя. На рис. 4 изображен поезд, дающий сигнал при движении по направлению к наблюдателю О1. В результате звуко­вые волны перед поездом сгущаются, и длина волны сокращается; длины волн, распространяющихся в обе стороны, не изменяются; волны, распространяющиеся назад, удлиняются. С каждой новой посылаемой волной поезд оказывается ближе к наблюдателю 01, чем он был в момент испускания предыдущей волны; следователь­но, каждой новой волне приходится проходить меньшее расстоя­ние, чем предыдущей. В результате к наблюдателю 01 приходит большее количество волн в секунду, чем это было бы, если бы поезд оставался неподвижным. Частота увеличивается, и повышается тон свистка. Как изменяются частота и высота звука для наблюда­телей O2 ? О 3 ? 04 ?

Кажущееся изменение высоты звука., вызываемое относительным движением источника и наблюдателя, называется эффектом Доп­лера. Вообще высота тона звучащего тела больше естественной ча стоты, когда источник звука и наблюдатель приближается Друг к Другу. Когда они удаляются друг от друга, звук понижается. Приведите примеры этого эффекта на основании вашего личного опыта

Резонанс. В предыдущей главе мы приводили доказательство того, что звук может производить работу. Но как получается, что рояль воспроизводит тот же са­мый тон, который вы напевали? Причина в том, что тон вашего голоса совпадает с частотой, кото­рая свойственна струне рояля. Это интересное явление называет­ся резонансом. Для его иллю­страции воспользуемся двумя ка­мертонами одинаковой частоты (рис.5).

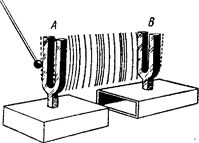
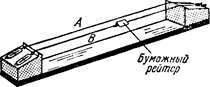
(рис.5 Явление резонанса) (рис.6 Демонстрация резонанса при помощи сонометра)

Когда камертон A начинает колебаться, он посылает в воздух чередующиеся сгущения и разре­жения. Первое сгущение, дости­гающее камертона. В, создает небольшое давление на ножки камер­тона и слегка смещает их. Наступающее следом разрежение позво­ляет ножкам вернуться в исходное положение. Поскольку В имеет ту же самую собственную частоту, что и -4, каждое последующее сгущение и разрежение от А способствует увеличению амп­литуды колебаний В. Таким образом, В вскоре начинает из­давать слышимый звук. Такие колебания называются «ответ­ными», или резонансными, коле­баниями. Они возникают благо­даря явлению резонанса (т. е. «ответа на звук»).

Резонансные колебания можно продемонстрировать также при помощи сонометра (рис. 6), на который натянуты две струны так, что частоты их одинаковы. Если возбудить щипком струну A, то рейтер па струне В подскакивает. Почему? Почему иногда во время грозы дрожат стекла в окнах?

Вы могли заметить, что между дощечками ксилофона подвешены пустые цилиндры, и, наверное, не могли догадаться, зачем они там. Цилиндры имеют различную длину, возрастающую от высоких тонов к низким. Простой опыт позволит нам понять роль этих резонаторов.

Поднесем вибрирующий камертон к высокому стеклянному цилиндрическому сосуду (рис.7). Будем теперь понемногу наливать воду в сосуд; через некоторое время мы услышим силь­ный звук. Если продолжать наливать воду, то звук прекратится.

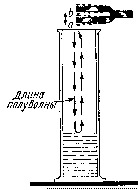
(рис.7 Резонанс в открытой трубе)

Повторим опыт, применив камертон более высокого тона. Те­перь оказывается необходимым налить больше воды, чем прежде, для того чтобы получить резонанс. Иначе говоря, необходимо уменьшить столб воздуха над водой для того, чтобы он стал колебаться созвучно с камертоном. Как это объяснить?

Пусть а, и Ь — крайние положения ко­леблющейся ножки камертона. Когда нож­ка переходит из положения Ь в положение а, то она посылает сгущение в цилиндр. Если мы хотим, чтобы звучание камертона усилилось, то это сгущение должно отра­жаться водой обратно, к ножке как раз вовремя, чтобы соединиться со сгущением, образовавшимся над ножкой при ее колеба­нии обратно в направлении к Ъ. Так как движение ножки от Ъ к а составляет поло­вину полного колебания, то расстояние вдоль цилиндра вниз и обратно должно составлять половину длины волны возбуждае­мого зпука. Таким образом, длина воздушного столба должна составлять четверть длины волны. Диаметр цилиндра также влияет на длину необходимого столба воздуха. Для получения длины, равной четверти длины волны (I) звука, необходимо добавить две пятых диаметра (и) цилиндра к длине (Г) столба воздуха. Тогда

Что такое биения и как они возникают? Выше уже указывалось что звуковые волны могут испытывать интерференцию

и если они имеют одинаковую длину волны, то могут усиливать или уничтожать друг друга в зависимости от того, встречаются ли они в одинаковых или противоположных фазах. Но что получается, если два камертона различных частот звучат рядом?

На рис. 29.8, а мы видим, что два таких камертона посылают волны различной длины. Волны камертона В короче волн камер­тона А. На рис. 29.8, Ь приведен график результирующей волны. Эти волны попеременно испытывают интерференционное усиление и ослабление, в результате чего. получаются попеременно области более интенсивного звука и тишины или почти тишины. Таким

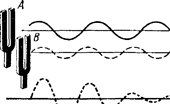
(рис.8 Попеременное усиление и ослабление звука создает биение)

образом, кажется, что звук появляется в виде отдельных импульсов, или биений. Биения получаются в результате интерференции звуковых волн неодинаковой частоты.

Для демонстрации биений можно воспользоваться двумя ка­мертонами одинаковой частоты. Ножка одного из камертонов должна быть слегка нагружена, в результате чего частота этого камертона окажется несколько меньшей, чем частота другого. Если заставить оба камертона звучать вместе, то будут слышны биения. В чем состоит закон биений? Повторим описанный выше экспери­мент, но увеличим нагрузку уже нагруженного камертона. Теперь биения окажутся более частыми, чем ранее. Очевидно, чем больше разность частот между камертонами, тем быстрее происходят бие­ния. Число биений, слышимых за секунду (короче, частота биений), равно разности между частотами колебаний звучащих тел. Это и есть закон биений ).

Что называется гармонией? Если продолжать описанный экс­перимент достаточно далеко, то можно получить столь быстрые биения, что они станут неразличимыми для уха. Можно услышать раздельно и сосчитать не более 4—6 биений в секунду. Когда частота биений достигает 16—20 в секунду, то они уже перестают быть слышимыми как отдельные импульсы. Ухо воспринимает их как новый тон, и если этот топ слышен наряду с двумя исходными, то он становится очень неприятным и раздражающим. Это явление низы пустея диссонансом.

Однако если число биений и секунду увеличить настолько, что отношения частот звучащих тел приблизятся к отношению частот у мажорной гамме, то получающийся в результате звук будет при­ятным, или гармоничным. Это явление называется консонансом, или гармонией. Можно представить себе те осложнения, которые получились бы, если бы мы попытались вообразить себе биения и комбинации биений, возникающие в результате всех возможных музыкальных аккордов. Пифагор в VI веке до нашей эры сделал первую попытку классифицировать гармоничные сочетания и по­казать, почему они оказываются консонантными или диссонантпыми. Однако консонанс для одного лица может оказаться диссо­нансом для другого.

Каковы законы колебании струн или проволок? Некоторые из вас знакомы с теми факторами, которые определяют частоты коле­баний струн, применяемых в струпных инструментах. Мы знаем, что скрипач нажимает пальцем па струпу далеко от верхнего порожка для того, чтобы сыграть высокую ноту; мы знаем, что увеличение натяжения струны повышает ее тон и что длинные толстые струны издают низкие топы. Эти наблюдения показывают, что частота струны зависит от се длины, натяжения и диаметра. Она также зависит от материала струны, т. е. от ее плотности или массы на единицу длины. Эксперименты показывают, что

частота колебаний струн или проволок: а) обратно про­порциональна их длине, б) прямо пропорциональна квад­ратному корню из натяжения струны, в) обратно пропорцио­нальна диаметру н г) обратно пропорциональна квадратному корню из плотности.

Каким образом столбы воздуха возбуждают тоны? Если пред­ставится возможность, посмотрите внутрь большого органа, вы увидите там много интересного и поучительного. Трубы органа различны по длине — от 5 см до 6 м и более. Некоторые трубы сделаны из дерева, а другие из металла; некоторые имеют квадрат­ное сечение, другие — круглое. Колебания столбов воздуха для возбуждения тонов происходят и в других музыкальных инструментах, но изучение органных труб поможет нам понять принципы возбуждения тонов всех духовых инструментов.

На рис. 29.10, а показано поперечное сечение открытой трубы, на рис. 29.10, с — закрытой трубы. В каждом случае столб воз­духа приводится в колебание путем вдувания воздуха сквозь щель 8 через ребро тонкого деревянного или металлического язычка L.

Это заставляет воздух колебаться туда и обратно через язычок и вызывать сгущения и разрежения, быстро распространяющиеся в'трубе туда и обратно — так же, как это происходило в нашем опыте, демонстрировавшем резонанс.

В открытой трубе воздух может свободно колебаться на про­тивоположном конце а. Области максимальных колебаний назы­ваются пучностями; они соответствуют гребням или впадинам поперечных волн (рис. 29.10, Ь). Сгущения отражаются от откры­тых концов трубы в виде разрежении, а разрежения отражаются в виде сгущений. Отраженные волны встречаются в середине тру­бы так, что образуется некоторая точка п, по обе стороны от кото­рой колебательные движения воздуха имеют противоположное на­правление. Таким образом, в этой точке, называемой узлом, нет никаких колебаний.

Изучение рис. 29.10, Ъ показывает, что длина волны равна четы­рехкратному расстоянию от пучности до узла. Сплошной линией на рисунке показана часть волны (апа), образующаяся в открытой трубе. Таким образом, длина открытой трубы равна половине дли­ны волны возбуждаемого звука.

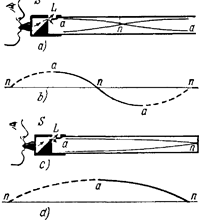
(рис.10 a) открытая труба, b) часть волны в открытой трубе, c) закрытая труба, d) часть волны в закрытой трубе)

В закрытой трубе воздух не может свободно колебаться у за­крытого конца. Поэтому здесь образуется узел, а у открытого конца получается пучность. На рис. 10, с и а показано, что длина, закрытой трубы рав­на четверти длины волны воз­буждаемого звука. Поскольку частота обратно пропорциональ­на длине волны, высота тона закрытой трубы на октаву ни­же тона открытой трубы той же длины. Заметим, что длина волны закрытой трубы (рис. 10, с1) вдвое больше длины волны открытой трубы. Приме­няя трубы различной длины, мы находим, что, чем короче труба, тем выше частота, и обратно.

Что такое обертоны? При рассмотрении струн и столбов воз­духа мы считали, что они колеблются как целое. Однако на самом деле их колебания значительно сложнее, чем это кажется на пер­вый взгляд. Легко показать, что они могут колебаться частями или отрезками.