Реферат: Функціональне відображення поведінки споживача

де матриця коефіцієнтів є матрицею Гессе, що облямована цінами, тобто

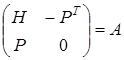, де – вектор-рядок.

Припустимо, що . Розв’язок (2) знайдемо за методом Крамера. При фіксованому значенні одержимо

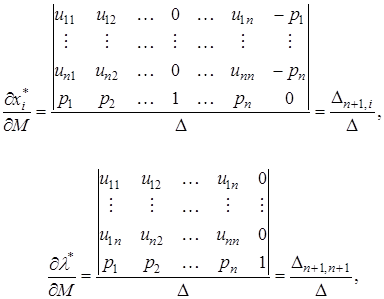
де – алгебраїчні доповнення елементів , відповідно.

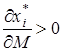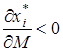
Якщо , то -й товар називається коштовним (цінним), при збільшенні доходу попит на цей товар також збільшується. На випадок, коли -й товар називається малоцінним.

2. Розглянемо вплив зміни ціни одного товару, наприклад 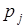, на поведінку споживача. Диференціюючи (1) по 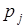, одержимо:

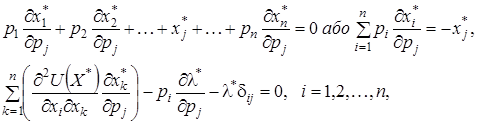(3)

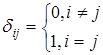де – дельта Кронекера . Запишемо систему (3) у такому вигляді:

.

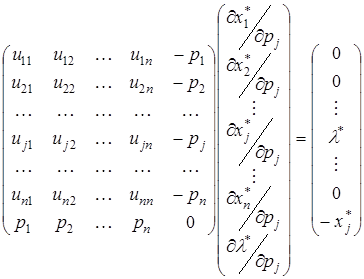Якщо матриця коефіцієнтів невироджена, тобто, тоді маємо при фіксованому такий розв’язок, який називають рівнянням Слуцького

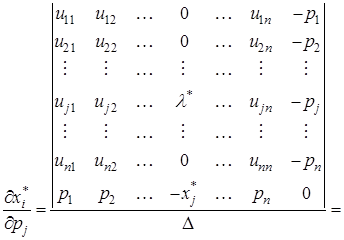
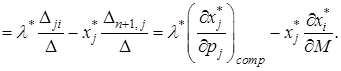(4)

Рівняння (4) є основним рівнянням у теорії цінності. Вираз 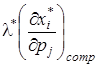називається коефіцієнтом Слуцького. З рівняння Слуцького випливає, що при змінюванні ціни на -й товар зміна попиту на -й товар наведена двома доданками, перший одержав назву ефекту заміни, другий – ефекту доходу. Отже: « Загальний ефект = вплив заміни + вплив доходу». Наприклад, при зниженні ціни на -й товар відбувається зростання доходу (ефект доходу), але він іде не повністю на закупівлю -го товару – частина його витрачається на закупівлю інших товарів (ефект заміни).

Нехай розв’язок (4) справедливий для всіх та таких, що , тоді матриця розміром симетрична й від’ємно визначена, тобто .

Можна встановити властивості цієї матриці.

Діагональні елементи виражають чистий ефект заміщення, тобто визначають зміну , яка є результатом варіації ціни , за умови, що доход підтримується на такому рівні, що значення залишається незмінним.

При товари та прийнято вважати взаємозамінюючими, при – взаємодоповнюючими, а при – незалежними.

3 Коефіцієнт еластичності

Коефіцієнтом еластичності функції одного аргументу називається величина, отримана в результаті ділення відносного приросту функції на відносний приріст аргументу. Позначаючи еластичність через , маємо за означенням

,

де – приріст аргументу;

– викликаний ним приріст функції.

Звичайно праву частину помножують і ділять на 100% та говорять, що коефіцієнт еластичності показує, на скільки відсотків змінюється значення функції при зміні аргументу на 1%.

При маємо

.

Якщо функція є функцією декількох аргументів, то говорять про часткові коефіцієнти еластичності

.

Функція попиту є векторною функцією, її можна розглядати як сукупність функцій попиту на окремі товари , кожна з яких є функцією від змінної. Отже, для кожної з цих функцій існує частковий коефіцієнт еластичності.

Залежно від типу аргументу розрізняють коефіцієнти еластичності за цінами й доходом.