Реферат: Функціональне відображення поведінки споживача

Показники , що характеризують аналогічно зміну попиту від доходу, називаються еластичністю за доходом.

4 Алгоритми розв’язання задачі споживання

Умови Куна-Такера дають повну характеристику розв’язку, однак не містять конструктивного методу його пошуку. Одними з алгоритмів розв’язання задачі нелінійного програмування (ЗНП) є градієнтні методи.

Процес знаходження розв’язку ЗНП градієнтними методами полягає в тому, що, починаючи з деякої точки , здійснюється послідовний перехід до деяких інших точок, поки не буде знайдений прийнятний розв’язок задачі. При цьому градієнтні методи розділяють на два класи.

До першого класу відносять методи, в яких точки , що досліджуються, не виходять за межі області припустимих розв’язків задачі. Найпоширенішим з таких є метод Франка-Вульфа.

До другого класу методів відносять методи, під час використання яких досліджувані точки можуть як належати, так і не належати області припустимих значень (метод Ероу-Гурвіца, метод штрафних функцій).

Під час знаходження розв’язку задачі градієнтними методами ітераційний процес здійснюється до того моменту, поки градієнт функції в черговій точці не стане дорівнювати нулю або ж поки

,

де – достатньо мале позитивне число, що характеризує точність отриманого розв’язку.

Для чисельного розв’язування задачі споживача використовуватимемо метод Франка-Вульфа.

Нехай потрібно знайти максимальне значення функції корисності за умови .

Характерною рисою даного методу є те, що обмеженням в задачі є лінійна нерівність. Ця особливість є основною для заміни нелінійної цільової функції лінійною поблизу досліджуваної точки, завдяки чому розв’язування задачі зводиться до послідовного розв’язання задач лінійного програмування.

Наприкінці першого розділу наведемо алгоритм методу Франка-Вульфа:

1. Процес знаходження розв’язку задачі починається з визначення точки, що належить області припустимих розв’язків задачі.

2. Знайдемо градієнт цільової функції в точці

.

3. Побудуємо лінійну функцію

.

4. Знайдемо максимум при обмеженні , тобто розв’яжемо задачу лінійного програмування (ЗЛП), звідки визначимо вектор , що доставляє максимум .

5. Визначимо значення оптимального кроку обчислення за формулою

.

6. Обчислимо компоненти нового припустимого розв’язку за формулою

.

7. Знайдемо значення , .

8. Порівняємо отримані , з точністю . Якщо , тоді і алгоритм переходить до пункту 2, якщо , тоді отримано оптимальний розв’язок задачі і при 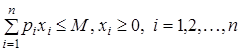.