Реферат: Гармоническая линеаризация
При увеличении амплитуды (![]() ) к уменьшается. АФХ не будет охватывать точку "-1", амплитуда колебаний убывает, система станет устойчивой. Следовательно, автоколебания, в точке "-1" будут устойчивыми.
) к уменьшается. АФХ не будет охватывать точку "-1", амплитуда колебаний убывает, система станет устойчивой. Следовательно, автоколебания, в точке "-1" будут устойчивыми.
Пример 2. Для заданной системы (рис.7) определить наличие автоколебаний и определить их устойчивость.
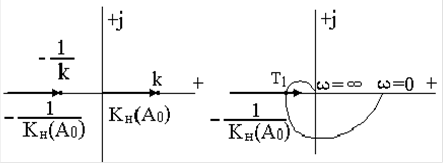
Рис.7
Рассмотрим линейную модель системы (рис.8).
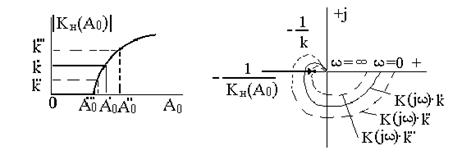
Рис.8
При увеличении амплитуды входного сигнала ![]() колебания возрастают, следовательно, цикл неустойчивый.
колебания возрастают, следовательно, цикл неустойчивый.
Выводы:
1. Для определения возможности существования предельных циклов находят точки пересечения характеристик К (j w) и ![]() .
.
2. Предельный цикл будет устойчивым, если изображающая точка на характеристике ![]() при увеличении
при увеличении ![]() не охватывается АФХ.
не охватывается АФХ.
3. Предельный цикл будет неустойчивым, если изображающая точка на характеристике ![]() при увеличении
при увеличении ![]() охватывается АФХ.
охватывается АФХ.
Пример 3. Для заданной системы (рис.9) определить наличие автоколебаний и определить их параметры и устойчивость при заданных параметрах системы: T = 0,1 c; k = 10 c-1 ; b = p /4.
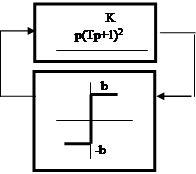 |
zx
![]() Рис. 9
Рис. 9
Решение: Определим выражение для АФХ линейной части
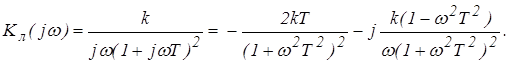
Определим частоту предельного цикла ![]() из условия
из условия
![]()
Определим
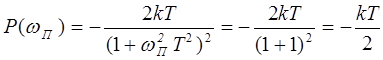 .
.
Условия гармонического баланса:
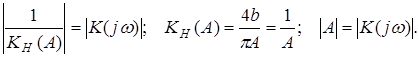
где ![]() - амплитуда предельного цикла.
- амплитуда предельного цикла.
Периодическое решение устойчиво. ![]()
Устойчивость предельного цикла можно определить из условия:
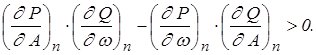
Пример 4. Для заданной системы (рис.10) определить наличие автоколебаний и определить их устойчивость.
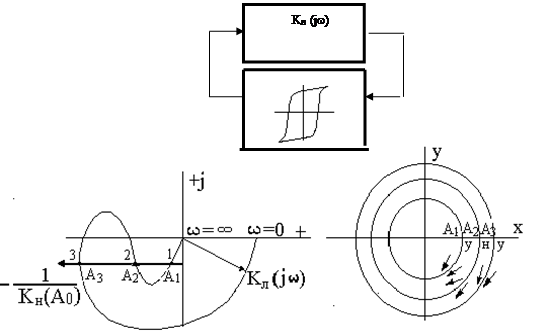 |
???.10 (?, ?, ?)
В этой системе могут существовать колебания трех различных амплитуд и частот. В точке 3 самая маленькая амплитуда и самая большая частота.