Реферат: Гармоническая линеаризация

Предмет: Теория Автоматического Управления

Тема: Гармоническая линеаризация

Метод гармонического баланса

Назначение: Метод гармонического баланса (гармонической линеаризации) - это один из наиболее распространенных инженерных методов, позволяющий определить наличие предельных циклов и определить их параметры и устойчивость.

Условия применения:

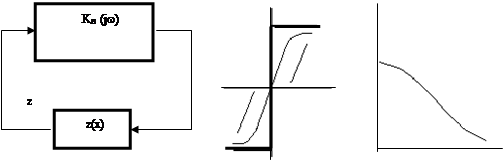
1. Нелинейную систему можно представить, состоящей из двух частей: линейной части - и нелинейного элемента (рис.1a).

2. Нелинейный элемент является безынерционным и имеет центрально-симметричную характеристику (рис.1б).

3. Линейная часть обладает хорошими фильтрующими свойствами в области низких частот (рис.1в).

a) б) в)

Рис.1

Рассмотрим разомкнутую систему (рис.2). На вход нелинейного элемента поступает гармонический сигнал. На выходе нелинейного элемента сигнал уже не гармонический, следовательно, его можно разложить в ряд по гармоническим составляющим.

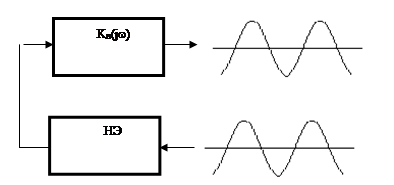???.2

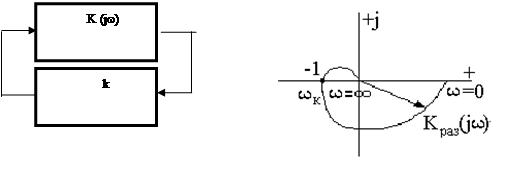
В этом разложении будут только нечетные гармоники, так как характеристика нелинейного элемента нечетная. Эти составляющие поступают на вход линейной части, которая обладает хорошими фильтрующими свойствами, т.е. пропускает только первую гармонику, все остальные будут сильно подавлены. Таким образом, на выходе линейной части получен тот же гармонический сигнал, что и на входе нелинейного элемента. Будем считать, что линейная часть является идеальным фильтром, при этом всю систему, в определенном смысле, можно рассматривать как линейную, и применять методы теории линейных систем, например, критерий Найквиста. Определение устойчивости предельных циклов методом гармонического баланса. Пусть задана система, состоящая из линейной части с АФХ - К (j w) и некоторого безынерционного звена с коэффициентом усиления - к ( рис.3а). При этом

. (1)

Если АФХ разомкнутой линейной системы проходит через критическую точку ( - 1, j0), то замкнутая система находится на границе устойчивости (рис.3б). При этом в соответствии с (1)

б)

?) ?)

Рис.3

Если система состоит из линейной части и нелинейного звена, то условия возникновения колебаний выглядят следующим образом (рис.4а)

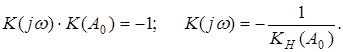(2)

Это условия называется условием гармонического баланса, т.е. выполняются условия: баланса амплитуд; баланса фаз.

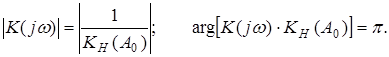(3)

Т. е. в точках пересечения К (j w) и выполняются условия баланса, при этом в системе возникают автоколебания (предельные циклы). В отличии от линейных систем, они могут быть устойчивыми и не устойчивыми. Количество точек пересечения определяет количество предельных циклов, а значения амплитудыA _{0 i} и частоты w_{0 i} в точках пересечения определяет параметры автоколебаний (рис.4б).

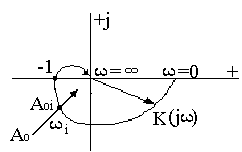
а)

Рис.4

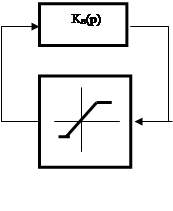
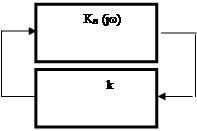
Пример 1. Для заданной системы (рис.5) определить наличие автоколебаний и определить их устойчивость.

?) ?)

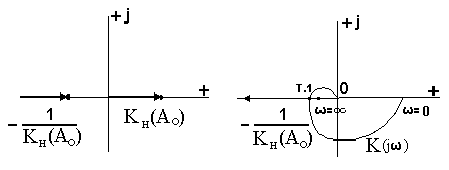Рис.5

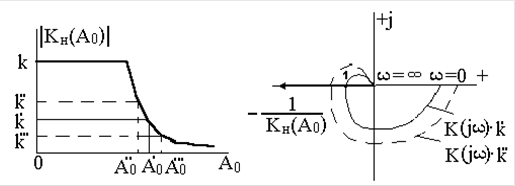
Так как характеристики пересекаются, то в этой системе возможны автоколебания, т.е. выполняются условия гармонического баланса. Эту систему можно представить в виде некоторой линейной (Рис.6).

Это возможно, если амплитуда равна При этом АФХ будет проходить через точку - 1. Если уменьшить амплитуду, т.е. , то к увеличится. Характеристика охватывает точку "-1", система не устойчива.

а)

а)

б) в)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--