Реферат: Геометрический способ сложения сходящихся сил
На практике рассматривают только острые углы, а знак проекции определяют непосредственно по чертежу. Например, 
.
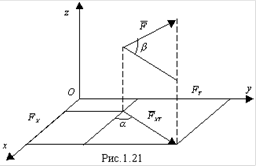
Проекция силы на плоскость. Проекцией силы F на плоскость Оxy называют вектор F xy , заключенный между проекциями начала и конца силы F на плоскость Оxy (рис.1.21). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная. По модулю F xy = F cosb где b - угол между направлением силы F и ее проекции F xy .
Проекция силы на ось, когда сила и ось не лежат в одной плоскости. В этом случае удобнее пользоваться следующим приемом:
а) проецируют силу F на плоскость, содержащую данную ось (например, на ось х-плоскость xOy);
б) найденную проекцию силы на плоскость проецируют на данную ось (ось х). Это и дает искомую проекцию силы на ось. В случае, изображенном на рисунке 1.21, найдем, что:
(1.9)
Этот метод называется методом двойного проецирования.
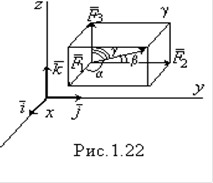
Разложение силы по координатным осям. Операция разложения силы обратна операции сложения сил (см. рис.1.17). Следовательно, чтобы разложить силу F по координатном осям x,y,z, необходимо на силе F , как на диагонали, построить прямоугольный параллелепипед, ребра которого параллельны данным осям x,y,z (рис.1.22)
По формуле диагонали параллелепипеда имеем:
F = F 1 + F 2 + F 3 (1.10)
где F 1 , F 2 , F 3 - составляющие силы F параллельные осям x.
Если орты осей координат i , j , k то: F 1 = i F x , F 2 = j F y , F 3 = k F z (1.11) где F x , F y , F z - проекции силы F на оси x,y,z. Подcтавляя (1.11) в (1.10), получаем: F = i F x + j F y + k F z . (1.12)
Формула (1.12) называется формулой разложения силы F по координатным осям. Проекции силы на оси координат определяются по формулам:
. (1.13)
Формула (1.12) справедлива при разложении любого вектора по координатном осям.
Аналитический способ определения силы по ее проекциям на координатные оси x,y,z. Если известны проекции силы на координатные оси x,y,z (риc.1.22), то модуль силы определим по формуле как диагональ прямоугольного параллелепипеда:
, (1.14)
а ее направление - по трем направляющим косинусам:
. (1.15)
Аналитический способ определения равнодействующей системы сходящихся сил. Пусть на твердое тело действует сходящаяся система сил (F 1 , F 2 ,... F n ). В таком случае равнодействующая этой системы сил определяется по формуле (1.6), т.е. равна геометрической сумме данных сил:
.
Спроецируем это векторное равенство на оси прямоугольных координат и найдем проекции равнодействующей:
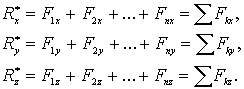(1.16)
Величина равнодействующей силы определится, согласно формуле (1.14), так:
, (1.17)
а направление - по трем направляющим косинусам: