Реферат: Геометрический способ сложения сходящихся сил
В результате для плоской системы параллельных сил остаются два уравнения равновесия:
Fiy = 0; 
MO (F i ) = 0.
Другая форма уравнений для такой системы сил, вытекающая из общих уравнений (II), имеет вид:
MА (F i ) = 0; MВ (F i ) = 0.
При этом точки А и В не должны лежать на прямой, параллельной силам.
Плоская система сходящихся сил.
В этом случае, когда линии действия всех сил пересекаются в одной точке, их моменты относительно этой точки равны нулю.
В результате получаем следующие уравнения равновесия:
Fix = 0; Fiy = 0;
то есть для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на координатные оси Ox и Oy были равны нулю.
Задачи статики на равновесие тела под действием плоской системы параллельных или сходящихся сил будут статически определимыми, если в них содержится только две скалярных неизвестных. Подробное изложение матричного метода составления уравнений равновесия твердого тела под действием плоской системы сил, а также примеры и исходные данные для выполнения индивидуальных заданий, дано в учебном пособии (глава 2):
Пример. Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н · м; расстояние а = 1 м.
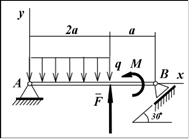
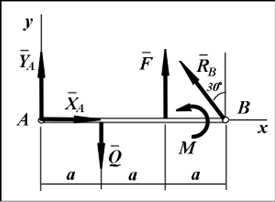
Решение. Введем систему координат Oxy, совместив начало координат О с неподвижным шарниром А и направив осьOx вдоль балки.
Для определения опорных реакций рассмотрим равновесие балки. К ней приложены активные силы: F , пара сил с моментом М и равномерно распределенная нагрузка. Заменим распределенную нагрузку ее равнодействующей Q , равной по модулю Q = q · 2a = 30 Н и приложенной в средней точке участка ее действия.
На балку наложены две связи: неподвижная шарнирная опора в точке А и подвижная шарнирная опора (каток) в точке В. Отбросим мысленно эти связи, заменив их соответствующими реакциями. Реакция R A неизвестна по величине и направлению, поэтому разложим ее на две неизвестные по величине составляющие X A ,Y A , направленные по координатным осям. Опора в точке В не препятствует ее перемещению вдоль наклонной плоскости и, следовательно, реакцию R B следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине.
Таким образом, в задаче имеется три неизвестных скалярных величины: XA , YA , RB . Поскольку для произвольной плоской системы сил имеется три независимых уравнения равновесия, данная задача является статически определимой. Составим уравнения равновесия балки под действием плоской системы сил, содержащей заданные активные силы и неизвестные реакции связей, в форме (II):
Fix = 0; MА (F i ) = 0; MВ (F i ) = 0.
Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:
Fix = XA - RB sin 30° = 0; (1)
MА (F i ) = - Q · a + F · 2a + M + (RB cos 30°) · 3a = 0; (2)
MВ (F i ) = - YA · 3a + Q · 2a - F · a + M = 0. (3)
Эта форма уравнений в данном случае обладает тем преимуществом, что каждое из двух уравнений моментов не содержит реакций, приложенных соответственно к моментным точкам А и В (так как их плечи относительно этих точек равны нулю). Напомним, что алгебраические моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции R B относительно точки А выделена ее вертикальна составляющая, равная RB cos 30° и имеющая плечо 3a, а горизонтальная составляющая имеет нулевой момент относительно точки А.
Из уравнений (2) и (3) находим
RB = (Q - 2F - M/a) / (3cos 30°) 
-50.0 Н;
YA = (2Q - F + M/a) /3 13.3 Н.
Полученное отрицательное значение RB означает, что сила R B направлена противоположно тому направлению, которое показано на рисунке.
Для проверки можно составить уравнение проекций сил на ось Oy, которое должно удовлетворяться при найденных значениях YA и RB :
Fiy = YA - Q + F + RB cos 30° = 13.3 - 30 + 60 - 43.3 = 0.