Реферат: Гирокомпас Вега
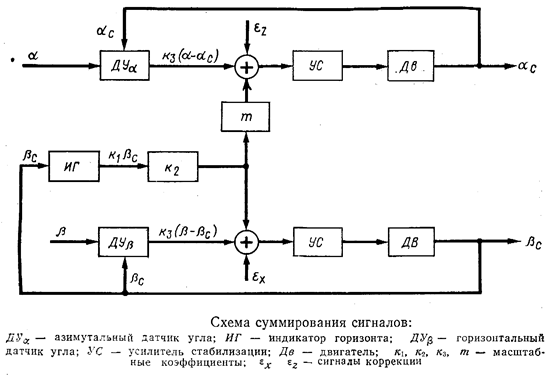
Один из возможных вариантов схемы суммирования сигналов показан на рис. 1.2. Эта схема, в которой применен индикатор горизонта с большой постоянной времени, позволяет осуществить следующее суммирование сигналов:
k3( b— bс ) - k1 k2 bс =0 (1. 2)
k3( a - a c ) – m k1 k2 bс =0 (1. 3)
где k3 – крутизна сигнала датчиков угла;
k1 – крутизна сигнала индикатора горизонта;
k2 и m – масштабные коэффициенты.
Для простоты постоянную постоянную времени индикатора горизонта не учитываем.
Обозначив через n= k1 k2/( k1 k2+ k3 ) , преобразуем выражения (1. 2)и(1. 3) в равенства:
( b— bс )= n b ; ( a - a c )= mn b , (1. 4)
из которых следует, что на вход усилителей следящих систем поступает управляющий сигнал, пропорциональный углу b . Кроме того, на схеме суммирования показана возможность введения в систему сигналов коррекции eх и e z , о выборе которых будет сказано ниже.
 |
Имея в виду, что частота собственных колебаний следящих систем значительно больше частоты собственных колебаний гиро-сферы, а переходный процесс в них затухает очень быстро, в уравнениях движения гирокомпаса можно оперировать соотношениями(1.4), которые не учитывают динамики следящих систем. Подставляя равенства (1.4) в выражения (1.1), получим уравнения, идентичные уравнениям обычного гирокомпаса с физическим маятником.
Анализируя эти уравнения, нетрудно найти, что период собственных колебаний гирокомпаса определяется выражением
Т = 2 p . V H / Cг n u cos j , (1. 5)
а коэффициент затухания :
h =Cв m n /H. (1. 6)
Очевидно, что величины периода колебаний и коэффициента за-гухания зависят не только от кинетического момента гиросферы Н и жесткостей Сг и Св, но и от коэффициентов п и т, характеризующих масштаб моментов, прикладываемых к гироскопу, по отношению к углу отклонения главной оси гироскопа от плоскости горизонтаb . Если в обычном маятниковом гироскопе момент прямо пропорционален углу b , а величина его равна Р1 b , где Р1— максимальный маятниковый момент, то в гирокомпасе с электромагнитным управлением зависимость момента от угла b определялась бы выражением Р ln b .
Меняя коэффициент п, можно изменять масштаб маятникового момента, а меняя коэффициент т — масштаб демпфирующего момента, и тем самым изменять величину периода незатухающих колебаний и коэффициента затухания.
Такая принципиальная и техническая возможность позволяет сравнительно просто решать следующие задачи:
ускоренное приведение гирокомпаса в меридиан, для чего необходимо уменьшить период незатухающих колебаний:
получение приемлемой точности курсоуказания при маневрировании, для чего, как известно, нужно увеличить период.
Для уменьшения периода коэффициент n следует увеличивать, а для увеличения периода — уменьшать.
Изменение коэффициента п можно осуществлять в схеме суммирования путем изменения масштабного коэффициента k2 , который специально введен в схему, поскольку коэффициенты k1 и k3 для данной конструкции постоянны. Однако при такой схеме суммирования, которая показана на рис.2, диапазон изменения коэффициента п ограничен.
Действительно, преобразуя выражение для n к виду
n=1/(k3 / k1k2+1) (1. 7)
нетрудно убедиться, что при увеличении k2 величина n приближается к единице. Это означает, что крутизна момента не может быть больше жесткости горизонтальных торсионов Сг, которая и будет определять величину наименьшего периода собственных колебаний гирокомпаса.
Что же касается наибольшего периода, то его величина ограничивается практически значениями возмущающихся моментов, которые возникают вследствие статических ошибок следящих систем и нелинейности характеристик датчиков угла и индикатора горизонта. При соизмеримости величин этих моментов с управляющими моментами система теряет свои качества и становится неработоспособной.
Работа следящих систем. Для правильного функционирования гирокомпаса наряду со схемой управления существенным является надлежащая работа следящих систем, от которых требуется высокая точность и большое быстродействие. Эти требования вытекают, как следствие, из самого принципа работы гирокомпаса, устройство которого рассмотрено выше.
Азимутальная н горизонтальная следящие системы выполняют в гирокомпасе две основные функции:
управление гироскопом путем наложения моментов через торсионы, которые непрерывно удерживаются закрученными на определенный угол;
слежение за гироскопом путем отработки всех угловых перемещений корпуса прибора, которые передаются на следящую сферу, вызывая рассогласование между гироскопом и следящей сферой.
При угловых перемещениях судна карданов подвес вместе с корпусом прибора как бы обкатывается вокруг гироскопа, который в режиме гирокомпаса, благодаря своим свойствам, остается неподвижным относительно системы координат, связанной с Землей, если не принимать во внимание переносного движения вместе с судном.
Наличие статических ошибок в следящих системах приводит к наложению на гироскоп возмущающих моментов, величины которых прямо пропорциональны статической ошибке и жесткости торсионов. В результате этого в показаниях прибора возникают погрешности, допустимые значения которых могут быть получены лишь при весьма малых статических ошибках следящих систем.
Воздействие на прибор всякого рода периодических несимметричных возмущений, например качки, может привести к появлению постоянных составляющих в динамических ошибках следящих систем и, как следствие, к дополнительным погрешностям в показаниях прибора. Поэтому к следящим системам гирокомпаса должны предъявляться очень высокие требования.
Что касается влияния собственных колебаний следящих систем на работу гирокомпаса, то поскольку частота этих колебаний значительно больше частоты собственных колебаний гиросферы, а переходный процесс в следящих системах при правильном выборе параметров затухает очень быстро, влияние колебании следящих систем практически не должно сказываться.
Однако выбранная для двухрежимного курсоуказателя конструктивная схема подвеса ЧЭ обусловливает взаимное влияние азимутальной и горизонтальной следящих систем при наличии наклонов следящей сферы вокруг оси ее подвеса, совпадающей с осью кинетического момента гироскопа—с осью уу (см. рис.1).
При таких наклонах, благодаря жесткой связи гиросферы со следящей сферой посредством торсионов, оси горизонтальных и вертикальных торсионов будут рассогласованы с осями приложения моментов от соответствующих двигателей на некоторый угол g.
Упрощая физику явления и принимая во внимание малость углов закрутки горизонтальных ( b— bс ) и вертикальных ( a - a c ) торсионов, измеряемых датчиками угла, и приведенных углов поворота осей двигателей горизонтальной db и азимутальной da стабилизации, связь между этими углами можно выразить формулами:
( b — bс )= d b cos g + d a sin g g . ; ( a - a c )= d a cos g + d b cos (1. 8)
Формулы (1.8) характеризуют взаимное влияние горизонтальной и азимутальной следящих систем при наклоне следящей сферы. Как показывает анализ, наличие перекрестных связей приводит к неустойчивости следящих систем, если не принять специальных мер. Наиболее простым способом, обеспечивающим устойчивость системы при любых углах g , является полное устранение перекрестных связей путем включения в контуры следящих систем преобразователя координат. В качестве преобразователя координат используется синусно-косинусный вращающий трансформатор (СКВТ), который включается в цепи следящих систем между датчиками угла и усилителями по схеме, показанной на рис.3.
Поступающее на входные обмотки преобразователя координат напряжение U, пропорциональное углам закрутки соответствующих торсионов, будет связано с приведенными углами поворота осей двигателей следующими уравнениями:
d b =U b cos g + U a sin g ; d a = U a cos g + U b sin g (1. 9)
в которых напряжение U b пропорционально углу ( b— bс ) и U a пропорционально углу ( a - a c ) .