Содержание

Введение

Ядерные силы являются короткодействующими. Это заключение основано на опытах по рассеянию заряженных и незаряженных частиц ядрами.

Приемлемые значения размеров зеркальных ядер, получен­ные в предположении, что разность их энергий связи обусловлена только электростатическим взаимодействием, свидетельствуют, по-видимому, о том, что гипотеза зарядовой независимости ядерных сил не находится в противоречии с эксперименталь­ными фактами.

Мы уже обращали внимание на то, что весьма важным свой­ством ядерных сил является свойство насыщения, проявляю­щееся в постоянстве плотности ядерного вещества почти во всех ядрах и в линейном возрастании энергии связи с увеличением массового числа.

Существование дейтрона — устойчивой системы протона и незаряженного нейтрона – свидетельствует о наличии действую­щих между ними сил неэлектрического характера. Эти силы не могут быть силами чисто магнитного взаимодействия (хотя оно и не исключается), поскольку такое взаимодействие не может обусловить среднюю энергию связи нуклона, составляющую около 7,5 Мэв.

Опыты по рассеянию нейтронов протонами указывают на за­висимость ядерных сил от спинов нуклонов. Существование элек­трического квадрупольного момента дейтрона и неаддитивность магнитных моментов протона и нейтрона в дейтроне указывают на тензорный характер ядерных сил. Кроме того, взаимодейст­вие между нуклонами может зависеть и от скоростей нуклонов.

Все перечисленные факты должны быть учтены при изуче­нии природы ядерных сил и должны быть объяснены теорией.

Изотопический спин

Известно, что протон и нейтрон являются двумя различными зарядовыми состояниями нуклона. Зарядовое состояние, описывается с помощью зарядовой координаты t, принимающей два значения: +1/2 для протон­ного и -1/2 для нейтронного состояния, подобно тому как спино­вая переменная s может принимать два значения, соответствую­щие двум возможным значениям проекции вектора спина на заданное направление. Эта аналогия между спиновой и зарядо­вой координатами позволяет использовать математический ап­парат теории спина.

Вводится либо оператор зарядовой координаты t с компо­нентами являющимися такими же матрицами, как и компоненты оператора спина s_x, s_y и s_z, либо оператор изотопического спина , который связан с t соот­ношением:

подобно тому как оператор Паули связан с оператором спина S.

О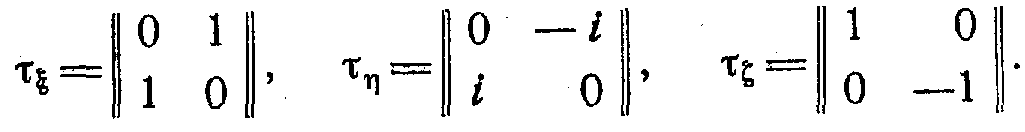ператор изотопического спина имеет, как и оператор Паули – три компоненты — матрицы , ничем не отли­чающиеся от матриц Паули:

«Пространство » — пространство изотопического спина, — од­нако не следует смешивать с обычным координатным про­странством, с которым может быть связано направление обыч­ного спина.

Операторам можно дать физическую интерпретацию; для этого введем два новых оператора , связанных с , следующим образом:

В матричной форме эти операторы имеют следующий вид:

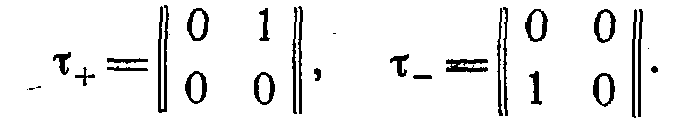
Каждый нуклон описывается двухкомпонентной функцией, кото­рую можно представить в виде матрицы-столбца. Протонное и нейтронное состояния нуклона описываются соответственно функциями

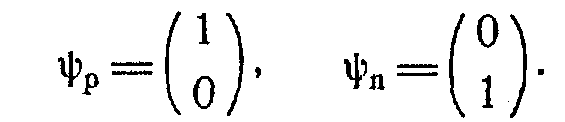
Действие операторов на функции описы­вается следующими соотношениями:

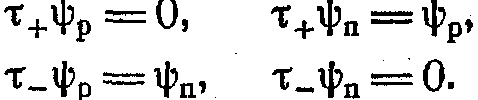
Таким образом, оператор «уничтожает» протонное состояние и «превращает» нейтрон в протон, а оператор _ «уничтожает» нейтронное состояние и «превращает» протон в нейтрон.

Оператор действует на следующим об­разом:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--