Ядро, состоящее из А нуклонов (A=Z+N), характеризуется оператором изотопического спина

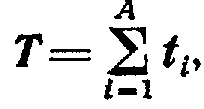
являющимся вектором в изотопическом пространстве. Абсолют­ная величина Т этого вектора согласно закону сложения кван­товых векторов может принимать значения 0, . . . , А/2. -компонента изотопического спина ядра равна

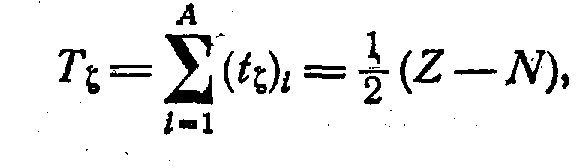
так как сумма всех протонов равна Z/2, а сумма нейтро­нов –N/2.

Абсолютная величина Т вектора изотопического спина не может быть меньше абсолютной величины проекции его на ось Ј, т. е. , и поэтому должно выполняться неравенство:

Это означает, что ядро может иметь равный нулю изотопи­ческий спин Т только в том случае, когда число протонов Z равно числу нейтронов N. Изотопический спин ядра может быть равен единице, либо когда число протонов равно числу нейтро­нов, либо когда число протонов отличается от числа нейтронов на единицу.

Изотопический спин системы, состоящей из двух нуклонов, может быть равен либо единице, либо нулю. Если Т=1, то может принимать три значения: -1, 0, +1. Значению Т= - 1 соответствует система, состоящая из двух нейтронов (каждому, нейтрону соответствует ); значению Т=0 соответствует система, состоящая из протона и нейтрона (заряд равен +1). При Г=1 заряд системы равен +2, т. е. система состоит из двух протонов. Итак, изотопическому спину Г= 1 соответствует изо­барный триплет n – n, n – р, р – р. Все. компоненты этого три­плета, состояния которых удовлетворяют принципу Паули ) , имеют одинаковые спины, четности и одинаковую внутреннюю структуру.

Таким образом, при T=1 возможны только такие состояния системы n – р, которые могут иметь место для систем, состоя­щих из двух протонов или двух нейтронов: 'S₀, (³Po, ³P, ³P) , т. е. только четные синглеты и нечетные триплеты. При T=0 существует только одно значение -компоненты изотопического спина: T. Этому состоянию системы двух нуклонов соответ­ствуют симметричные волновые функции , т. е. чет­ные триплеты и нечетные синглеты.

Приведенная классификация состояний дает возможность бо­лее четко сформулировать сущность зарядовой незави­симости, т. е. изотопической инвариантности ядерных сил, для системы, состоящей из двух нуклонов: ядерное взаимодействие любой пары нуклонов в состояниях с Т= 1 одинаково.

Гипотеза изотопической инвариантности ядерных сил осно­вана на предположении, что в изотопическом пространстве от­сутствуют физически выделенные направления: трехмерное изо­топическое пространство изотропно.

Представление об изотопической инвариантности легко мо­жет быть обобщено на случай более сложных систем, состоящих из Z протонов и N нейтронов. В случае строгого выполнения изотопической инвариантности гамильтониан системы не дол­жен меняться при замене любого протона на нейтрон и наоборот. Все состояния системы, в которой произведена такая за­мена, должны совпадать с состояниями первоначальной системы, если только они не запрещены принципом Паули .

Замена протона нейтроном означает уменьшение Т на еди­ницу, т. е. поворот вектора Т в изотопическом пространстве. Если в результате такой замены гамильтониан не изменится, то он инвариантен относительно вращения в изотопическом про­странстве. Изотопический спин системы в этом приближении является интегралом движения, т. е. он сохраняется. Каждому состоянию системы соответствует определенный изотопический спин Т, зависящий от изотопических спинов всех частиц, обра­зующих систему, и от их ориентации в изотопическом про­странстве.

В действительности протоны по своим свойствам (по массе, электрическому заряду, магнитному моменту) несколько отли­чаются от нейтронов, поэтому замена протона нейтроном и наоборот должна приводить к изменению гамильтониана системы. Это означает, что изотопический спин Т не является точным «квантовым числом. Вследствие кулоновского взаимодействия в гамильтониан должны войти члены, не инвариантные относи­тельно вращений в изотопическом пространстве. Однако в лег­ких ядрах, содержащих небольшое число протонов, кулоновское взаимодействие значительно слабее ядерного, благодаря чему зарядово-неинвариантные члены гамильтониана можно рассмат­ривать как малое возмущение. Такое возмущение приводит к тому, что состояние системы может являться смесью состояний с различными значениями изотопического спина. При очень малых зарядово-неинвариантных членах состояние системы можно характеризовать изотопическим спином, играющим роль неточного квантового числа. Из анализа экспериментальных данных следует, что для невозбужденных состояний ядер изотопический спин имеет смысл квантового числа вплоть до Z20. Легкие ядра можно разбить на две группы: ядра с целым и полуцелым изотопическим спином Т (т. е. ядра соответственно с четными и нечетными A). Каждому значению Т соответствует 2Т+1 возможных значений проекции изотопического спина Т, образующих изотопический мультиплет. Целочисленному изотопическому спину Т соответствует нечетное, а полуцелому — четное число компонент мультиплета.

С увеличением Г энергетическая устойчивость ядер уменьшается, поэтому основным состояниям ядер соответствуют малые значения изотопического спина: Т=0, 1/2 и 1. В зависимости от значения изотопического спина системы можно говорить об изобарных синглетах (Т = 0), дублетах (Т=¹/₂) и триплетах (Т=1). К изобарным синглетам относятся такие ядра, как ₂Не⁴ и Н². Это можно обосновать следующим образом. Ядру ₂Не⁴, со­стоящему из четырех нуклонов, соответствует компонента T =0. Следовательно, у ₂Не⁴ изотопический спин Т может быть равен 0, 1 или 2. Если бы изотопический спин ₂Не⁴ был равен 1 или 2, то существовали бы такие ядра, как ₄Н⁴ и ₄Ве⁴, причем их энер­гии связи, согласно гипотезе изотопической инвариантности, не­значительно отличались бы от энергии связи ₂Не⁴. Такие ядра, однако, не существуют, и это свидетельствует о том, что изото­пический спин ₂Не⁴ равен нулю. Можно показать, что равен нулю изотопический спин дейтрона, ₃Li⁶, 5В¹⁰, ₆С¹², ₇N¹⁴, 8О¹⁶.

Зеркальные ядра 1H³ и ₂Не³ можно рассматривать как ядра, образующие изобарный дублет. Для этих ядер изотопический спин может принимать значения ¹/2 или ³/₂, так как Т = ±¹/₂. Однако значение Т=³/2 должно быть отброшено, поскольку при Т=³/₂ существовали бы устойчивые системы из трех протонов или трех нейтронов. Оказывается, что для основных состояний всех ядер с нечетным А вплоть до ₁₇Cl³³ T=¹/₂.

Такие ядра, как ₄Ве¹⁰, ₅В¹⁰, ₆С¹⁰, образуют изотопический триплет, соответствующий трем возможным значениям проек­ции изотопического спина Т=1, причем ядру ₄Ве¹⁰. соответствует Т= – 1, ₅В¹⁰ — Т = 0 и 6С¹⁰ – Г = + 1.

Протон и нейтрон можно рассматривать как частицы, обра­зующие нуклонный дублет. Изотопический спин t нуклона ра­вен 1/2, причем протонному состоянию соответствует компонента Т = +¹/₂, а нейтронному Т = — 1/2 Это позволяет выразить за­ряд Z нуклона (Z равен единице для протона и нулю для ней­трона) через -компоненту изотопического спина:

Эта формула может быть обобщена на случай, когда система состоит из нескольких нуклонов, получим:

Таким образом, заряд ядра выражается через Т и число нуклонов, входящих в состав ядра.

Обменные силы

Явление насыщения и короткодействующий характер ядер­ных сил впервые были объяснены на основе предположения об обменном характере ядерных сил, т. е. что эти силы возникают между двумя частицами благодаря обмену третьей частицей. Такой частицей в случае взаимодействия нуклонов яв­ляется, по-видимому, мезон. Если состояние двух взаимодей­ствующих нуклонов зависит от их пространственных r1, r₂ и спиновых s1, s₂ координат, то подобный обмен может осуще­ствляться тремя различными способами.

1) Нуклоны могут обмениваться пространственными коорди­натами, сохраняя неизменными спиновые переменные. Эта воз­можность была рассмотрена Майорана. Силы, возникающие при таком взаимодействии, получили название сил Майорана.

2) Возможен обмен нуклонов спиновыми переменными при неизменных пространственных координатах. Этот вариант был рассмотрен Бартлеттом. Силы взаимодействия нуклонов при таком обмене получили название сил Бартлетта.

3) Возможен одновременный обмен спиновыми и простран­ственными координатами. Возникающие при этом обменные силы известны под названием сил Гейзенберга.

Формальное описание обменного взаимодействия осуще­ствляется путем введения в гамильтониан системы таких опера­торов, которые, действуя на волновую функцию, вызывают пере­становку координат или перестановку спинов, либо и тех и других одновременно в зависимости от характера обменных сил.

В случае обменных сил Майорана оператор энергии взаимо­действия может быть представлен в виде произведения V(r)P_M, где V(r) — функция, зависящая от расстояния между нуклона­ми, а Pm — оператор, меняющий местами пространственные ко­ординаты, входящие в волновую функцию: