Реферат: Імітаційна модель взаємодії підприємства з ринком

г) d = 0,2 ; p_i = 0,015 ;t _i = 1; х_{i 0} = 0,012 ; х_{i 0} (t₀ ) = 0,4;

д) d = 0,2 ;p_і = 0,015 ;t_і =1; х_{i 0} = 0,015 ; х_{i 0} (t₀ ) = 0,4.

Розглянемо вплив зміни тривалості виробничого цикла t( при фіксованих інших параметрах) на обсяг пропозиції і-го суб’ єкта ринку х_i . Чим коротше виробничий цикл товара, тим скоріше будут ь обертатися вкладені у виробництво кошти. Так, якщо підприємству вдається скоротити свій виробничий цикл ( при незмінних інших по казниках господарської діяльності ) , то його прибуток збільшиться. А ос кільки дана модель побудована, виходячи з припущення про те, що швидкість зміни пропозиції пропорційна швидкостізміни прибутку, то логічно зробити такий висновок : чим менше тривалість виробничого цикла підприємства, тим більше обсяг виробництва продукції. Іншими словами, хто швидше крутиться, той “крутіше”. Дана ситуація илюструється малюнком 2.2:

а) d = 0,2 ;p_i = 0,015 ;t_i = 1 ; х_{i 0} = 0,001 ; х_{i 0} (t₀ ) = 0,4;

б) d = 0,2 ;p_i = 0,015 ;t_і = 0,9 ; х_{i 0} = 0,001; х_{i 0} (t₀ ) = 0,4;

в) d = 0,2 ;p_і = 0,015 ;t_і =0,8; х_{i 0} = 0,001; х_{i 0} (t₀ ) = 0,4;

г) d = 0,2 ;p_i = 0,015 ;t_i = 0,7; х_{i 0} = 0,001; х_{i 0} (t₀ ) = 0,4;

д) d = 0,2 ;p_і = 0,015 ;t_і =0,5; х_{i 0} = 0,001 ; х_{i 0} (t₀ ) = 0,4.

В завершенні аналізу впливу параметрів системи на обсяг пропозиції необхідно також сказати про дефіцит ринку d. З ростом дефіциту на той чи інший товар, ціна на нього також буде змінюватися в сторону збільшення. Це означає, що прибуток, який отримує підприємство, буде збільшуватись. Отже, чим більший дефіцит на ринку, тим краще на ньому працювати підприємству.

3. Знаходження оптимального обсягу випуску продукції.

?? ???? ??????????? ?????? ????? ???????? ???????? ???????? ??????????? ?? ?????? ??????????????? ????????? ????? :
??????????? ????????? ???????????? ???? ???? ? ??????? ????????? ??????? ???????? ?_i0 <?_i <?_{i f} . ??? ????? ????????? ?_i ?????????? ???????????? ???? ????????? ????? ??????????? ?????? ??? ?????. ???????? ?????????? ??? ???????????? ? ????? ??????? ??? ????? ???? ?????????? ???????????? ????????. ??? ??????????? ???????????? ?????? ??????????? (??????????) ?????????? ??????? ?????? ??????????? ?_i ?? ??????? ??? ????? ?? ????????????:

З точки зору графічної інтерпритації це означає, що необхідно знайти прямокутник, одна сторона якого буде дорівнювати величині віпуску продукції x_i , а друга - різ ниці між ринковою ціною та собівартістю, тобто прибутку на одиницю продукції при такому обсязі виробництва, при цьому площа прямокутника повинна бути максимальною.

Знайдемо похідну цього виразу та прирівняємо її до нуля. Звідси отримаємо вираз для оптимального значення обсягу виробництва (пропозиції) і-го підприємства:

Цей вираз визначає такий об’єм пропозиції (виробництва) і-того підприємства, при якому величина прибутку цього підприємства буде максимальною. Але підприємству не завжди доцільно намагатися максимізувати прибутки в конкретний момент часу, тому що притримуючись такої стратегії можна втратити частину ринку. Така стратегія може бути застосована у випадку, коли підприємство зацікавлене в отриманні максимального прибутку в короткий термін з подальшим виходом з ринку. Наприклад, компанії терміново потрібні значні фінансові ресурси для покращення свого становища на основному ринку (підриву позицій конкурентів). Для цього вона може інвестувати кошти в інший бізнес, вклавши основну частину в оборотний капітал – закупівля сировини та матеріалів. При цьому звівши до мінімуму капітальні вкладення – придбавши не найкраще, а можливо й не нове обладнання. Це дасть змогу при необхідності вийти з ринку з найменшими втратами і швидко. Вираз “при необхідності” використано не випадково, оскільки обставини можуть скластися таким чином, що новий ринок буде більш привабливим і компанія взагалі переорієнтує свою діяльність.

З іншого боку, коли метою підприємства є тривале знаходження на даному ринку, така стратегія є недоцільною. В таких випадках компанії скоріше прийдеться відмовитися від ідеї швидко “відбити” вкладені кошти на користь зміцнення своїх позицій та збільшення долі ринку. Адже пануваня на ринку варте того, щоб трохи зачекати.

4. Кількість підприємств на ринку.

Розглянемо параметр конкурентноздатності підприємства р. Цей параметр характеризується структурою витрат підприємства. Під структурою витрат розуміється процентне співвідношення постійних і змінних витрат. Так, якщо валові витрати виробничих підприємств “А” і “В” співвідносяться в такий спосіб:

підприємство “А”	підприємство “В”
Постійні витрати	35%	60%
Змінні витрати	65%	40%
Валові витрати	100%	100%

то можна зробити висновок, що ці підприємства мають різну структуру витрат.

Типовою причиною такої різниці може бути те, що підприємство “А” має менший ступінь автоматизації і, отже, великою потребою у використанні ручної праці. Постійні витрати фірми “А” на амортизацію виплату відсотків на капітал, використаний на придбання устаткування, та інше в зв'язку з цим будуть достатньо невеликі, у той час як змінні витрати на оплату праці, навпаки, значними. З підприємством “В” справа полягає протилежною образом: значна частка постійних витрат у складі валових може свідчити про високий ступінь автоматизації, гарній підготовці кадрів, у тому числі й управлінського персоналу, і відповідно про незначні змінні витрати на оплату ручної праці. Очевидно, що підприємство “В” у даному випадку є більш конкурентоспроможним, ніж підприємство “А”. Подібна ситуація і характеризується його великим параметром конкурентноздатності р (при фіксованих інших параметрах).

Крім того, можна відзначити, що існують такі складові валових витрат, що не підлягають керуванню з боку керівництва підприємства, наприклад, податки, обов'язкові відрахування в соціальні фонди. І чим вище будуть їхні процентні ставки, тим складніше буде працюватися підприємству. Подібні витрати включаються в змінні витрати, а отже з їхнім ростом величина параметра р буде зменшуватися.

Розглянемо випадок чистої конкуренції. Спробуємо знайти зв’язок між параметром конкурентоспроможності р_і та кількістю підприємств на ринку n при умові, що всі інші параметри системи сталі та на ринку працює n однакових підприємств, тобто вони мають однакові параметри р_і = p, х_{i 0} = х₀ , х_i (t0) = x(t0), t_i . В цьому випадку рівні пропозиції всіх підприємств однакові і графіки, що ілюструють динаміку їх пропозицій однакові і зливаються в одну лінію (малюнок 4.1 ).

Проаналізуємо більш докладно цю ситуацію. Зі збільшенням кількості компаній на конкретному ринку, доля прибутку кожної з них буде зменшуватись. Оскільки будь-який ринок обмежений, то з зростанням його насиченості, при рівних можливостях підприємства, що працюють на ньому, будуть змушені ділити прибуток між собою на рівні частини, тобто чим більше суб’єктів, тим менша доля ринку припадає на кожного. Очевидно, що при деякій їх кількості, діяльність кожного з них стане збитковою.

??? ??????????? ??????? ??? n?? p_i ?????????? ????????? ???????, ???? ??????? ?????????? ?????? ?? ???????? ??????????? ????? ???? ???? ??????? ????? (???. 4.2). ? ????? ??????? ???????? ? ?????? (1.2):

Вираз (1.2) матиме вигляд:

Прирівняємо виробничі затрати Fта ціновий коефіціент C:

З цього рівняння отримуємо квадратне рівняння для точок перетину х. Оскільки нас цікавить випадок дотику, тобто коли рівняння має один розв’язок, прирівняємо дискримінант до нуля. Отримаємо вираз:

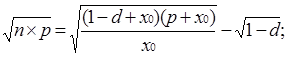Легко бачити, що вираз для nмає вигляд:

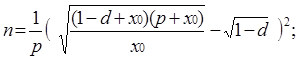Отже, ми отримали залежність між параметром конкурентоспроможності р_і та кількістю підприємств на ринку n. Взагалі конкурентоспроможність характеризує його якості у порівнянні з аналогічними товарами інших виробників і можливість продаватися на ринку за ціною не нижчою за середньоринкову. Більш конкурентоспроможний товар краще відповідає вимогам ринку і виробляється та продається, як правило, з меншими затратами. Існує багато шляхів зменшення витрат. Наприклад, підвищенням ефективності керування та використання ресурсів, впровадженням нових ресурсозберігаючих технологій, автоматизація процесу виробництва. Все це характеризується параметром р_і . Дійсно, чим більше р_і , тим ефективніше працює підприємство,бо його витрати на одиницю продукції менші.

На малюнку 4.3 зображено графік залежності n від p, при х₀ = ; d = 0,2. А на малюнку 4.4 графік логарифмічної залежності. Можемо бачити, що при p®0 кількість підприємств, що можуть працювати на ринку одночасно і отримувати прибуток, безмежно зростає. При збільшенні pдо безмежності гранична кількість підприємств прямує до певного значення.

Граничне значення nв цьому випадку дорівнює:

Мінімум функції (4.4) дорівнює 1. З формули (4.4) випливає, що значення р в цій точці дорівнює:

Це є те граничне значення параметру конкурентоспроможності, при якому відбувається перехід з області малих підприємств в область великих при збільшенні р.