Реферат: Інтегральні характеристики векторних полів

1. Диференціальні операції другого порядку

Нехай в області задані скалярне поле і векторне поле , причому функції мають в області неперервні частинні похідні другого порядку. Тоді і є диференційовними векторними полями, а – диференційовним скалярним полем.

До векторних полів і можна застосувати операції обчислення дивергенції і ротора, а до скалярного поля – операцію обчислення градієнта. Таким чином, отримуємо повторні операції:

.

Операцію називають оператором Лапласа і позначають також символом :

.

З допомогою оператора Гамільтона оператор Лапласа записується у вигляді

.

Враховуючи, що

,

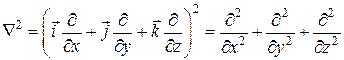дістаємо

.

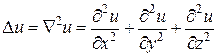Функція , яка задовольняє в деякій області рівняння Лапласа , називається гармонічною в цій області. Наприклад, лінійна функція є гармонічною в довільній області. Оператор Лапласа широко застосовується в рівняннях математичної фізики. Відзначимо, зокрема, що потенціал електричного поля точкового заряду або поля тяжіння точкової маси, який має вигляд , при задовольняє рівняння Лапласа:

(потенціальне векторне поле є безвихровим) і

(векторне поле є соленоїдальним).

1. Дві інші повторні операції і пов’язані співвідношенням

, (1)

де – вектор-функція, координатами якої є результати застосування оператора Лапласа до функцій .

2. Розкладання векторного поля на суму потенціального і соленоїдального полів

Довільне неперервно диференційовне векторне поле може бути зображено у вигляді

, (2)

де – потенціальне поле, – соленоїдальне поле.

Дійсно, за означенням потенціальне векторне поле є градієнтом деякого скалярного поля : . Тому для вектора із рівності (2) маємо

. (3)

Щоб векторне поле було соленоїдальним, воно має задовольняти умову , звідси, враховуючи рівність (3), знаходимо

.

Таким чином, для скалярного потенціала поля отримуємо рівняння

--> ЧИТАТЬ ПОЛНОСТЬЮ <--