Реферат: Інтегральні характеристики векторних полів

Нехай в області визначено векторне поле ; – замкнений контур, який лежить в області ; – довільна поверхня, межею якої є контур ; («поверхня натягнута на контур »); – одиничний вектор нормалі на обраній стороні поверхні .

Нехай функції та їхні частинні похідні першого порядку неперервні на поверхні . Тоді справедлива формула Стокса

,

де орієнтація контуру узгоджена з орієнтацією поверхні . Ліва частина формули Стокса є циркуляцією векторного поля вздовж контура , а права частина визначає потік через поверхню векторного поля з координатами 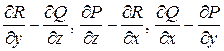, тобто потік через поверхню . Тому формулу Стокса можна записати у векторній формі:

(12)

або

. (13)

Фізичний зміст формули Стокса: циркуляція векторного поля вздовж замкненого контуру дорівнює потоку ротора векторного поля через поверхню, натягнуту на цей контур.

8. Властивості потенціального поля

Як відомо, векторне поле , яке задовольняє в області умову , називається потенціальним у цій області ( – скалярний потенціал поля ). Якщо поле потенціальне в області , то 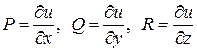і вираз 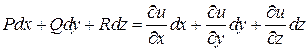є повним диференціалом функції в області . Це означає, що виконана умова незалежності криволінійного інтеграла від шляху інтегрування в просторі.

Таким чином, потенціальне в області поле має такі властивості.

1. Циркуляція потенціального поля вздовж довільного замкненого контуру дорівнює нулю:

.

2. Для довільних точок і області циркуляція потенціального поля вздовж кривої не залежить від вибору кривої і дорівнює різниці значень потенціала в точках і :

.

У випадку силового потенціального поля ця властивість означає, що робота такого поля вздовж кривої не залежить від вибору кривої, а залежить тільки від початкової і кінцевої точок і .

3. Потенціальне поле є безвихровим, тобто .

Нехай тепер дано векторне поле , яке задовольняє в області умову . Чи випливає звідси, що поле є потенціальним в області ? Відповідь на це запитання залежить від форми області . Якщо область є поверхнево однозв’язною, то із умови випливає, що існує функція така, що

.

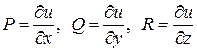Отже, , тобто поле є потенціальним в області .

Таким чином, умова є необхідною і достатньою умовою потенціальності поля у поверхнево однозв’язній області.

Потенціал потенціального поля у поверхнево однозв’язній області можна обчислити за формулою:

. (14)

Якщо область не є поверхнево однозв’язною, то умова не є достатньою для потенціальності поля в області .

9. Інваріантне означення ротора

Нехай в області визначено векторне поле . Зафіксуємо точку і деяку площину, яка проходить через цю точку. Нехай – одиничний вектор нормалі до площини, – замкнений контур, який лежить в площині і обмежує область таку, що – внутрішня точка області . Запишемо формулу (12) для векторного поля в області . Застосовуючи до правої частини цієї формули теорему про середнє, отримуємо

,

диференціальне векторне поле формула соленоїдальне