Реферат: Исследование и разработка конструкции бандажированного опорного валка стана 2500 горячей прокатки

В целом можно сказать, что в обоих случаях обеспечивается хорошая несущая способность соединения и достаточно небольшие напряжения в деталях валка, но более предпочтительным является бандаж, внутренний диаметр которого d=1150 мм, за счет значительного увеличения все той же несущей способности.

2.2 Расчет напряжений в бандажированном опорном валке

Напряжения в составном опорном валке стана 2500 определяются для тех же основных технических данных, заданных в пункте 2.1. Требуется определить контактные напряжения на посадочной поверхности бандажа и оси.

Область бандажа обозначим через S₂, а область вала через S. Радиус поверхности сопряжения после сборки обозначим R, а внешний радиус бандажа R₂.

На внешнем контуре бандажа C₂ приложена сила P, равная по величине давлению металла на валки P₀. Принимая P=P₀, имеем систему сил, находящихся в равновесии. Посадочная поверхность образует контур C.

Расчетная схема представлена на рисунке 5.

Рисунок 5 – Расчетная схема для определения контактных напряжений в валке

При решении задачи напряжения удобно определять в полярных координатах. Нашей задачей является определить:

_r – радиальные напряжения

_ - тангенциальные (окружные) напряжения

_r - касательные напряжения.

Вычисления компонентов напряжений обычно весьма громоздки в общем виде и в расчетах. Используя метод Н.И. Мусхелишвили применительно к поставленной задаче и выполняя решение аналогично приведенного в работе [10] определяются напряжения на посадочной поверхности бандажа в виде формул, удобных для численной реализации [11]. Окончательные выражения имеют вид:

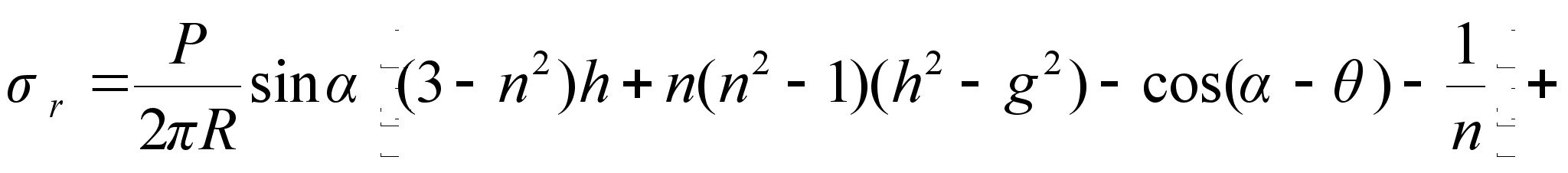
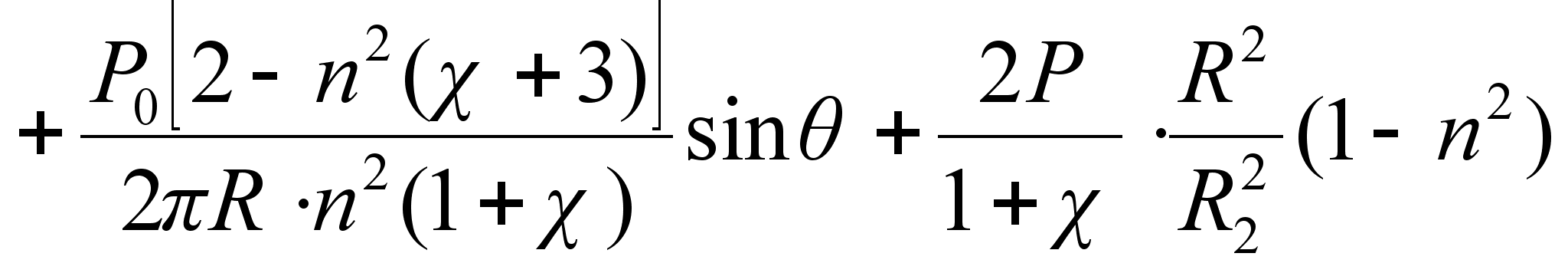
(9)

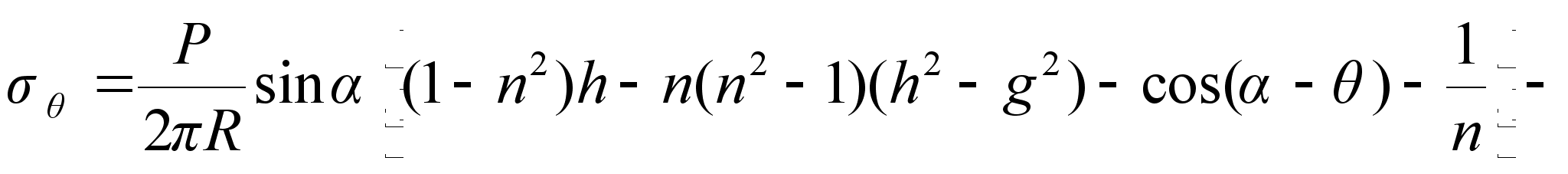
(10)

(11)

где P=P₀ – удельная нагрузка на единицу длины бандажа от внешней силы;

R – радиус контактной поверхности;

h и g – просуммированные в замкнутом виде ряды, отражающие особенность решения в зонах точек приложения сосредоточенных сил P и позволяющие улучшить сходимость рядов;

 - угловая координата точек контура C;

• постоянная Мусхелишвили;

=0,3 - коэффициент Пуассона;

 - угол, отсчитываемый от оси х, до точки приложения силы Р;