УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В ГОРОДЕ СТЕРЛИТАМАК

КАФЕДРА ЕСТЕСТВЕННО-НАУЧНЫХ И ОБЩЕПРОФЕССИОНАЛЬНЫХ ДИСЦИПЛИН

ИССЛЕДОВАНИЕ МЕТОДОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по ИНФОРМАТИКЕ

2403.302413.000ПЗ

(обозначение документа)

Группа ВТС-109	Фамилия, и. о.	Подпись	Дата	Оценка
Студент	Терещук А.И.
Консультант	Карасев Е.М.
Проверил

Стерлитамак 2011г.

Содержание

Введение

Теоретическая часть

Метод Симпсона (парабол)

Пример применения

Практическая часть

Программное вычисление

Визуализация методов

Заключение

Список литературы

Введение

При решении ряда актуальных физических и технических задач встречаются определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, в приложениях приходится иметь дело с определенными интегралами, сами подынтегральные функции которых не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.

Мне была поставлена задача исследовать два метода вычисления определенных интегралов: метод трапеций и метод Симпсона (парабол)

метод трапеция симпсон интеграл

Теоретическая часть

Метод трапеций

Пусть требуется вычислить интеграл 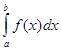. Разобьем сегмент на n равных частей при помощи точек . Метод трапеций заключается в замене интеграла 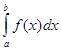суммой

площадей трапеций с основаниями, соответственно равными и , и с высотами, равными .

Таким образом, справедлива формула:

,

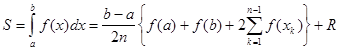Где R - остаточный член. Это формула называется формулой трапеций .

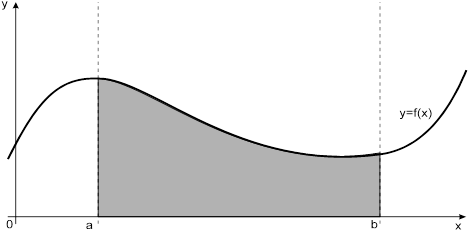
Рисунок 1 - Криволинейная трапеция

--> ЧИТАТЬ ПОЛНОСТЬЮ <--