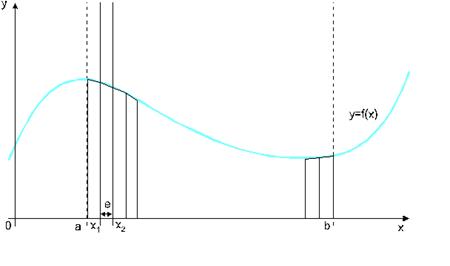
Рисунок 2 - Метод трапеций

Метод Симпсона (парабол)

Для вычисления интеграла 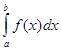снова разобьем сегмент на n равных частей при помощи точек и обозначим через середину сегмента . Метод парабол заключается в замене интеграла 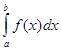суммой

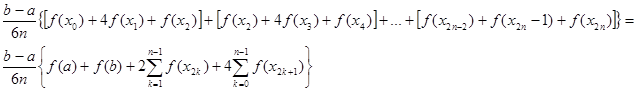площадей фигур и представляющий собой трапеции, лежащие под параболами, проходящими через три точки графика функции f ( x) cабсциссами .

Таким образом, справедлива формула:

,

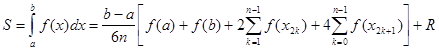Где R - остаточный член. Это формула называется формулой Симпсона.

Пример применения

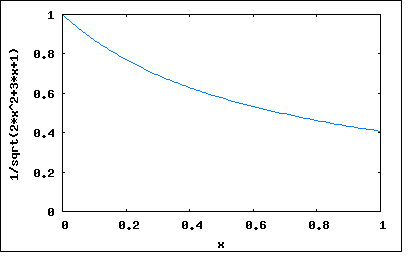
Рисунок 3 - График функции

	y0	y1	y2	y3	y4	y5	y6	y7	y8	y9	y10
x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
y	1	0,86	0,76	0,68	0,6	0,55	0,5	0,47	0,46	0,43	0,41

Найдем площадь криволинейной трапеции методом трапеций:

S=0,1* ( (1+0,41) /2+0,86+0,76+0,68+0,6+0,55+0,5+0,47+0,46+0,43) =0,6025 кв. ед

Найдем площадь криволинейной трапеции методом Симпсона:

S=0,0017*2* (1+0,41+2* (0,76+0,6+0,5+0,46) +4* (0,86+0,68+0,55+0,47+0,43)) =

=0,6123 кв. ед

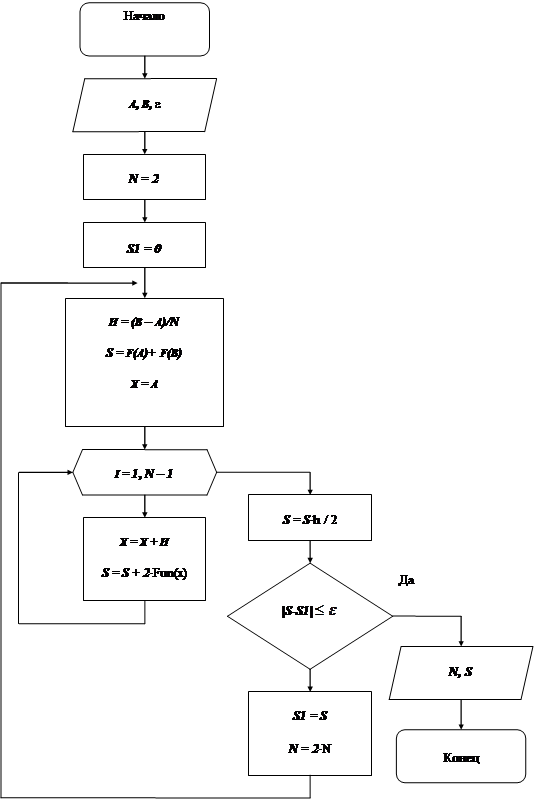Блок-схема метода трапеций

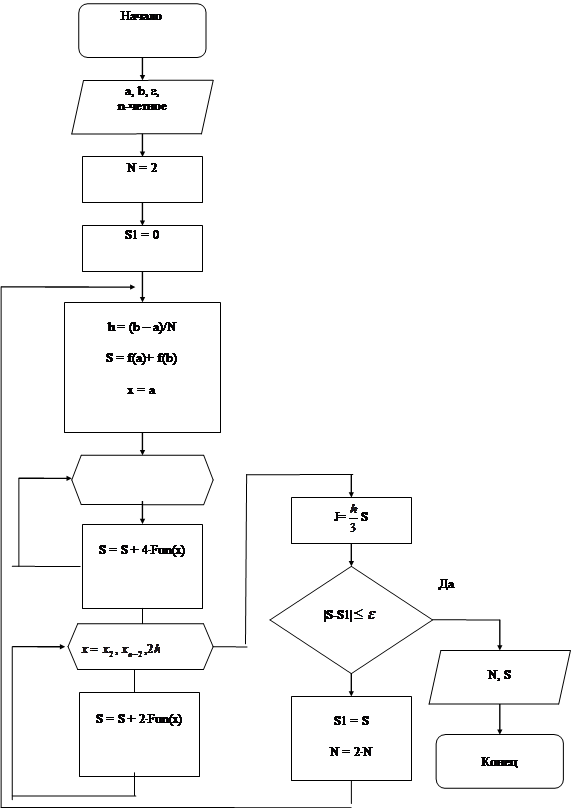Блок-схема метода Симпсона

Практическая часть

Конструирование интерфейса

Программа разрабатывается в объектно-ориентированной среде программирования Lazarus.

Перед началом программирования, была создана форма Заставка.

Рисунок 4 - Заставка

В этом окне расположены:

· Кнопка "Запуск", позволяющая приступить к началу программы;

· Компоненты Label;

Затем была создана основная форма Меню, позволяющая выбирать операции.

Рисунок 5 - Основная форма

Данное окно представляет главное окно программы.

В этом окне расположены:

· Компоненты Label для подписи компонентов Edit;

· Компонент MainMenuдля выбора операции;