Реферат: Исследование распределения температуры в тонком цилиндрическом стержне

В ряде практических задач возникает необходимость исследования распределения температуры вдоль тонкого цилиндрического стержня, помещённого в высокотемпературный поток жидкости или газа. Это исследование может проводиться либо на основе обработки эксперимента (измерение температуры в различных точках стержня), либо путём анализа соответствующей математической модели.

В настоящей работе используются оба подхода.

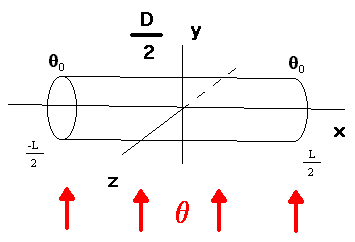
Тонкий цилиндрический стержень помещён в тепловой поток с постоянной температурой q, на концах стержня поддерживается постоянная температура q₀ .

1.2 Математическая модель

Совместим координатную ось абсцисс с продольной осью стержня с началом в середине стержня. Будем рассматривать задачу (распределения температуры по стержню) мосле момента установления режима Т₀ .

?????? ?????????????? ?????? ?????????? ????????????????? ??????, ??? ???? ???????? ??????????? U_i ??????? ? ?????????? ?????? ??????? ? ???????????? x_i . ?????????? ????????? U_i ????????????? ??? ??????? ????????? ? ???????? ??????????. ???????? ???????? U(x) ????? ?????? ?? ? ???? ?????????? ?? ?????? ???????? x (??????????? 4-?? ???????? ????? ??????????).
(1.1)

Задача сводится к отысканию оценок неизвестных параметров, т.е. коэффициентов a₀ , a₁ и a₂ , например, методом наименьших квадратов.

Вторая математическая модель, также использующая экспериментальные данные, состоит в применении интерполяционных формул и может употребляться, если погрешность измерений температуры Ui пренебрежимо мала, т.е. можно считать, что U(x_i )=U_i

?????? ?????????????? ?????? ???????? ?? ????????????? ?????? ???????????. ????? ????????, ??? ??????? ??????? U(x) ????? ???:

(1.2)

где l - коэффициент теплопроводности, a - коэффициент теплоотдачи, D – диаметр стержня, q - температура потока, в который помещён стержень.

???? U(x) ??? ??????? ??????? ?????? ??? ????????? (1.2) ? ?????????? ?????????:

(1.3)

на отрезке [-L|/2;L/2], где L – длина стержня, q₀ - постоянная температура, поддерживаемая на концах стержня.

Коэффициент теплопроводности lзависит от температуры:

(1.4)

где l₀ - начальное значение коэффициента теплопроводности, s_l - вспомогательный коэффициент.

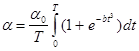??????????? ??????????? a ????????? ?? ???????:

(1.5)

?.?. ??? ??????? ???????? ???????

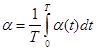за некоторый отрезок времени от 0 до Т, здесь a₀ - значение a при t стремящемся к бесконечности, b – известный коэффициент.

????? ?₀ , ?? ????????? ???????? ????????????? ??????????? ? ??????? ????? ??????? ?????????????? ???????????? ?? ???????:

(1.6)

??? ? ? ??????????? ??????????????????????, x - ?????????? ????????????? ?????? ?????????:

(1.7)

Задание курсовой работы

Вариант № 136

Исходные данные:

1. L = 0.0386 м

2. D = 0,00386 м

3. q = 740 ^о С

4. q₀ = 74 ^о С

5. l₀ = 141,85 (Вт/м*К)

6. s_l = 2,703*10^-4

7. B = 6,789*10^-7

8. a₀ = 3,383*102 (Вт/м² *К)

9. T = 218 ^о С

10. А = 3,043*10-5 (м² /с)

11

X, м	U, o C
0	353
0,00386	343
0,00772	313
0,01158	261
0,01544	184
0,01930	74

2 . Обработка результатов эксперимента.

2.1 Задача регрессии. Метод наименьших квадратов.

???? ??????? ????????? ? ???? (1.1). ?????? ????????????? ??????? ? ??????? ???, ??? ???? ??????????? ????? ??????, ?????????????? ??????? ????????? ?????????? ????????? ??????? ????????? ?? ????????????????? ???????? ???????????; ???????????? ????? ?? ???? ????????????????? ??????, ?.?. ??????? ???????? S: